911テロで考える、材料力学が役立つ理由:仕事にちゃんと役立つ材料力学(2)(1/2 ページ)
材料定数は環境によってドラマチックに変化し、製品生命を脅かす場合すらある。材料力学を学べば、その根拠も理解できるようになる。
本連載執筆のため、ひさびさに材料力学の書籍を購入しました。書店に足を運んでいる時間もないので、通信販売で購入しました。当然、書籍を手に取って内容を確認できないので、そのタイトルだけが選択基準です。なるべく分かりやすそうで、そそるタイトルのものを選びました。表紙はWebで見たとおり、なかなか親しめて、なおかつ、そそりました。
そして、中をパラパラっとめくってみたのですが……。
「変わってないよーっ!」
僕が学生時代に材料力学の単位を取得したときの教科書の内容とほぼ同じように、材料力学特有のたくさんの図とギリシャ文字を使った式がギッシリ並んでいました。
まあ、考えてみれば、材料力学は確立された1つの学問分野ですので、内容はそんなに大きく変わるハズはないのです。ともかく、この書籍を見て、僕が材料力学を初めて学んだときのことを思い出しました。「材料力学を理解することが、一体、何の役に立つんだ?」――僕の場合、まずそれがいまいちハッキリしませんでしたが、読者の皆さんはどうでしょう?
材料定数の変化って、怖い
材料力学ですから、“材料について分かる”のは当たり前ですよね。それでは、材料についていったい“何が”分かるのでしょうか?
材料にはその性質を表すさまざまなパラメータ(定数)があります。
- 材料の「硬さ」を表す定数
- 材料の「熱の伝わりやすさ」を表す定数
- 材料の「強さの限界」を表す定数
などなど……。
またこれらの材料の性質を表す定数は、いろいろな環境によって変化することがあります。時間が長く過ぎる(いわゆる「風化」です)とか、非常に高い温度にさらされるとかで、材料の性質は、時には劇的に変化します。
思い出すのもイヤな事件だったので、多くを語りたくはありませんが、「材料の性質を表す定数は一定ではない」という実例を以下で挙げたいと思います。
2001年9月11日、アメリカ同時多発テロ事件が発生しました。ハイジャックされた旅客機が世界貿易センタービル(通称:ツインタワー)に突っ込んだのです。その映像は、多くの人が目にしたことがあると思います。最初、ビルはモクモクと煙を上げていました。この時点で、誰がこのビルが倒壊して崩れ落ちると想像したでしょう?
航空機の空路も近い理由から、ツインタワーはボーイング707クラスの旅客機が衝突しても崩壊しないように設計されていたということです。ただしこれは、あくまで衝突のダメージのみを想定して設計されたもので、ジェット燃料の延焼による火災のダメージは想定されていなかったということです。
ツインタワーの建設にはもちろん鉄骨が使われています。ビルを支えている鉄骨の強度が、ジェット燃料の延焼熱によって、どんどん低下していったのです。そして高層階の重さを支え切れなくなって、崩壊してしまったのです。
このように、材料の性質を表す定数は環境によって大幅に変化します。その変化の度合いが、時に、製品の生命を脅かす領域に達することがあるのです。
材料力学をきちんと学ぶと、上に挙げたような「材料の性質」の意味が分かります。製品は必ずそれを作る材料があります。同じカタチなのに、頑丈だったり、すぐに壊れたりしますね? 材料の性質を知っているかいないかは、製品のカタチにも影響してきます。材料力学を学ぶ、すなわち「材料の性質を知る」ことにより、設計のバリエーションが広がるといっていいでしょう。
しかも材料の世界は日進月歩ですから、これまでは絶対ムリだったカタチの製品も、材料が進歩すれば可能になるかもしれないのです。
アタリ計算をする
材料力学の本を少しでも眺めたことがある人は、棒のような図がたくさん出てくることに気が付くと思います。材料力学や構造力学では、「片持ちばり」「両端固定ばり」というものをよく使います。ここでの「ばり」とは「梁(はり)」のことを表します。梁とは、一般的に「建築部材」を表す言葉ですが、建築設計だけではなく機械設計の力学計算の際の用語としても登場しますよね。
梁は、屋根に載っかるカワラや雪の重さを柱に伝える役目を持っています。一般的には、梁は水平に配置されます。そして柱は垂直に配置されます。梁は水平に配置されて、屋根の上に載っかったものの重さを柱に伝えます(図1)。
木造建築でも鉄筋コンクリート建築でも、梁と柱というものは必ず存在します。マンションにお住まいの方は、梁や柱をすぐに確認することができると思います。梁について、詳しくは以下のURLを参照してみてください。
材料力学や構造力学に出てくる絵は、水平に描かれているものがほとんどで、「○○ばり」と呼ばれます。
- 「片持ちばり」は、片方だけ固定された梁です。壁に非常に頑丈に固定された棒をイメージしていただければいいと思います
- 「両端固定ばり」は、棒の両方が固定された梁です。小学校のグラウンドにある鉄棒みたいなもんです
このような棒の状態で、そこに重さが加わったとき、棒の太さなどが分かれば、棒がどれくらい曲がるか、カンタンな数式で計算することができるわけです。
オリンピックの鉄棒や段違い平行棒などの競技で、選手が大車輪などをすると鉄棒がたわむのが分かりますよね。鉄棒の断面や長さと選手の体重が分かれば、カンタンな数式にこれらを代入するだけで、鉄棒がどれくらいたわむのか分かるのです。つまり皆さんが設計しているもので棒状のものがあれば、それに力や重さが加わったときに曲がる量が「だいたい」分かる、ということになります。試作品を作る前にカンタンな計算で設計したものがどれくらい曲がるのか分かれば、その分、設計が確かなものになります。
設計するものに重さや力が加わったときに、どれくらい曲がるのか、カンタンな数式で計算することを「アタリ計算」などということがあります。材料力学や構造力学を勉強すると、このようなアタリ計算ができるようになるというわけです。
「僕が設計しているものは、棒みたいにカンタンじゃないよ」
そんな声が聞こえてきそうですね?
でも、昔は(多分、現在でも)大きな船1隻も、1本の棒に置き換えてアタリ計算していたのです。それに棒だけじゃなく板の計算式もあります。CAEがいまのように“コンビニ”化する前は、すべて、この公式と計算尺だけで、設計したものの強度を検討してきたのですから。
アタリ計算ができるようになると、自分の設計を根拠あるものにすることができますし、CAEの結果を評価するためにも使えます。アタリ計算の公式については、この連載の中で実習を交えて紹介していきます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- 知らないと取り返しがつかなくなる金型の費用と作製期間の話
- 3σと不良品発生の確率を予測する「標準正規分布表」
- ムダのない作業と楽しさをもたらす“ありそうでなかった発想”
- 有限要素法入門 〜連立方程式の解法、変位の計算〜
- フローで考える流れのモデリング(その2) 〜適用例と3D/1Dの関係〜
- 幾何公差の基準「データム」を理解しよう
- 計算時間が従来比最大1000倍高速な流体解析ベースのトポロジー最適化ソフト
- Excelを使って周波数分析をやってみよう!
- 3D機構検証ソフトの最新版、干渉検証漏れ防止機能を搭載
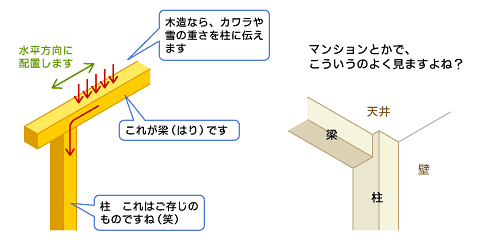 図1 梁とは?
図1 梁とは?

