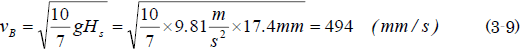ボールの運動軌跡が簡単に計算できるの?:ピタゴラスイッチの計算書を作ろう(3)(1/4 ページ)
ボールが滑っていく軌跡も計算で分かる。しかし本当にそうなる? シミュレーションと実験の結果を動画で比較してみた。
いよいよ、サブ・システム2の設計へ
今回は、サブ・システム1の曲線スロープを登ってきたボールが、サブ・システム2の直線スロープ1とゲートを通過して、サブ・システム3のロック機構を解除するため運動条件を求め、この条件を基にゲートを設計します。
銀二「今度はサブ・システム2の設計だね。設計条件は何だと思う?」
草太「『曲線スロープから登ってきたスーパーボールが直線スロープ1を降ってゲートを押しのけることができる』これが必要条件だね。ところで、ボールはどのくらいの速度で曲線スロープを登ってくるのかな?」
銀二「計算してごらんよ」
X年度 卒業設計課題(亜津戸大学 工学部 物田研究室)
図のようなピタゴラスイッチを設計・製作し、設計計算書と試作品を提出せよ。
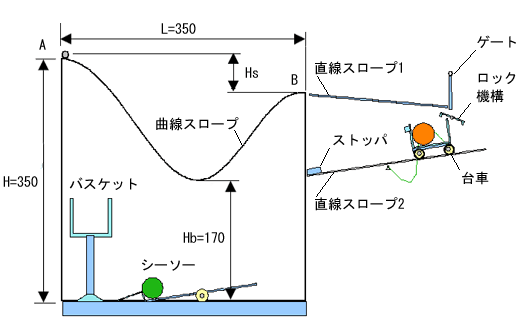
A地点から出発したボールは曲線スロープを経てB地点に到達し、直線スロープ1の終端のゲートを通過した後、直線スロープ2に繋留(けいりゅう)している台車のロックを解除する。
繋留が解除された台車は直線スロープ2を降り、ストッパによって横転し、台車の中のボールがシーソーに落下して、反対側のバスケットボールを跳ね上げ、バスケットの中に入るものとする。
なお、曲線スロープの出発地点Aの高さHとスロープの底の高さHb、曲線スロープの長さLは図示した値とし、また、B地点を通過するときのボールは極力遅くなるように設計すること。
編集部より、読者の皆さまへ
以降で出てくる数式をメモ帳やノートなどに書き取るなどして、実際に計算しながら読み進めてみてください。より理解が深まります。
草太「ここもエネルギー保存の関係を利用すると便利なんだね。第1回の曲線スロープでのエネルギー保存の関係式は、これだったね」
草太「で、スタート地点Aでは並進速度vAも回転速度ωAも、0とすると」
草太「ボールは摩擦係数の大きいスーパーボールだし、曲線スロープ終点Bでの傾斜はほぼ0だから、ボールが滑ることはないと考えていい。だから並進速度は回転速度で表すことができる。つまりボールの半径をrとして、vB=rωBだから、こう」
草太「従って、曲線スロープからB地点に到達するときのボールの角速度は、こうね」
草太「曲線スロープでのエネルギー損失は小さいと仮定するとEloss=0となる。さらにボールの回転速度ωBを並進速度vBに置き換える」
銀二「よくできたね。傾斜が大きいときは滑りやすく、傾斜が小さいときは滑りにくい。だから傾斜の小さいB地点では滑らないとしたのは、斜面での運動をよく理解している証拠だ」
草太「そりゃそうさ。第1回の内容をみっちり復習したからね」
銀二「ところで、100円ショップで買ってきたスーパーボールの質量と径はいくらだい?」
草太「質量は6.7gで、径は24mmだよ」
銀二「じゃあ、曲線スロープを登ってくるときの速度vBが分かるね」
草太「まずボールの慣性モーメントは(1-4)から、質量m、半径rに対して、こうなる」
だから……、
草太「へーえ!? ボールが回転しても、スロープの終点Bでのボールの速度はボールの質量にも大きさにも関係ないんだ。意外だなぁ」
銀二「数式を使うと、思いもしなかったことが分かることがあるから面白いんだ」
草太「ふーん。なるほどねぇ…それで、重力加速度9.81mm/s2とスロープの段差Hs=50mmを代入する」
=837 (mm/s) (3-6)
草太「結構速いね」
銀二「ちなみに、曲線スロープでエネルギー損失があるとして、前回の演習問題1のように転がり摩擦係数を0.05として計算したらどうなる?」
草太「前回の演習問題1で、転がり摩擦損失は位置エネルギー換算で
Eloss/(mg)=17.5mm
だったから(3-5)でHsの代わりに、50mm-17.5mm=32.5mmを代入する」
銀二「つまり、サブ・システム2の直線スロープ1には0から837mm/sの速度でボールが突入してくるってわけだ」
草太「なんで? 675mm/sじゃないの?」
銀二「『675mm/s』という速度は、転がり摩擦係数を0.05とした場合の値で、実際のところ、どの程度の値か分からんだろ? だから675mm/sという速度は目安にすぎないんだ。でも、この目安を持っておくことが重要なんだ」
草太「じゃあ、837mm/sはどうなの?」
銀二「この値は損失エネルギーがないとしたときの計算だろ? 実際、エネルギーは必ず損失するんだ」
直線スロープに突入するときの速度は837mm/sより遅いことが理論的に保証されます。つまり、どんなに速くても837mm/s以上になることはありません。理論計算で上限を押さえておくことは設計をするうえで非常に重要なポイントです。
草太「そうだよね。それに曲線スロープを登り切るんだから、絶対に0mm/s以上だよね」
銀二「ということで、具体的に設計してみようか」
草太「えっ? 直線スロープ1の設計ってどうするの?」
銀二「スロープの長さと傾斜角度が直線スロープ1の設計要目だけど、サブ・システム3のロック機構やその後の台車や直線スロープ2の配置関係など、全体とのバランスを考えてお前が好きに決めればいいさ」
草太「じゃあ、長さを『200mm』、傾斜をキリのいい値で『5°』としてみようか」
銀二「実際に図面に書いて、自分の目で確認した方がいいぞ。この辺は理論よりセンスだからな」
草太「図3.1を見る限り、いいんじゃないの?」
銀二「ついでに、ゲートも一緒に設計してしまおうか」
草太「ボールの直径は24mmだから、ゲートの高さはボールの径の2倍で48 mmぐらいかな。ゲートには使わなくなったネームプレートを使おうかと思っているんだ。丁度いい大きさなんで。それと、ゲートの回転ジョイントには吊り金具(『ヒートン』質量は0.9g)を使おうと思うんだ」
銀二「グッドアイデアだね。プレートの高さは42mmだね。じゃあ、ヒートンと組み合わせて、下面から回転中心までをキリのいいところで50mmとしてみたらどうだい」
草太「そうだね。ゲートはこんな感じかな」(図3.2)
銀二「ところで、直線スロープ1を通過してゲートと衝突するときのボールの速度はどうなる?」
草太「直線1のスロープ段差は、
200 mm×sin(5°)=17.4 mm
だから、曲線スロープの出発点Aから見ればゲートまでは、
50+17.4=67.4 mm
の段差だね。エネルギー損失を考えなければ、ゲートと衝突するときのボールの速度は(3-5)から、次のように計算できるね」
銀二「曲線スロープの終点Bでの速度が0だったら、ゲートとの衝突速度はどうなる?」
草太「その場合は段差17.4mmに対して(3-5)を使えばいいから、こうなるね」
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- 有限要素法入門 〜連立方程式の解法、変位の計算〜
- 3σと不良品発生の確率を予測する「標準正規分布表」
- ムダのない作業と楽しさをもたらす“ありそうでなかった発想”
- 知らないと取り返しがつかなくなる金型の費用と作製期間の話
- SUBARUが深層学習によるAI構築ツールを導入、プレス領域の成形解析工数の削減へ
- 幾何公差の基準「データム」を理解しよう
- フローで考える流れのモデリング(その2) 〜適用例と3D/1Dの関係〜
- 計算時間が従来比最大1000倍高速な流体解析ベースのトポロジー最適化ソフト
- 「設計者はなぜCAEを煙たがるのか」を考察し、広がりを阻害する壁を取り除く
 ピタゴラスイッチ
ピタゴラスイッチ
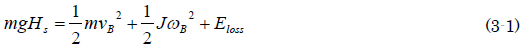
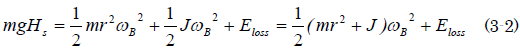


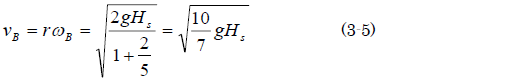
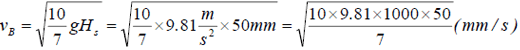
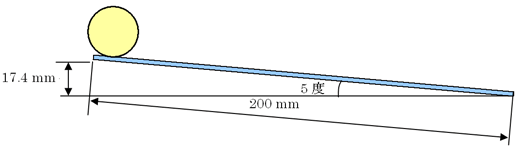 図3.1 直線スロープ1 構想図
図3.1 直線スロープ1 構想図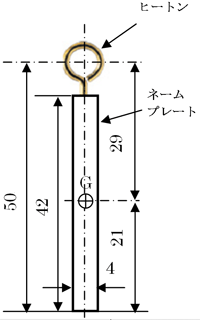 図3.2 ゲート構想図:「G」は重心を意味します
図3.2 ゲート構想図:「G」は重心を意味します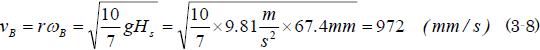
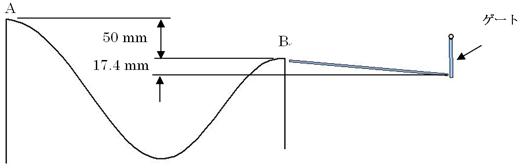 図3.3 出発点から ゲート突入点までの段差
図3.3 出発点から ゲート突入点までの段差