同軸かどうか寸法で表せないときは、神頼み!?:製図を極める! 幾何公差徹底攻略(8)(2/2 ページ)
同軸度
JISによると、「同軸度(Coaxiality)とは、データム軸直線と同一直線状にあるべき軸線のデータム軸直線からの狂いの大きさをいう」と定義されます。データム軸線と同軸であって欲しいという形体に対して指示するものです。
加工者が何も気にせず、作業がやりやすいよう、旋盤やフライス盤を使って加工すると同軸が崩れる可能性があります。設計意図を表すために、同軸性を要求する場合はその旨を加工者に伝える必要があります。
図4に示す図面例は、段付き軸の小径側の中心軸をデータムとし、大径側の中心軸がデータム軸と同軸となる直径0.03mmの円筒内にあれば合格品と判断されるものです。
それぞれの直径に寸法公差が記入されていますが、独立の原則に従うため寸法公差とは無関係に同軸度を満足させればよいということです。
対称度
JISによると、「対称度(Symmetry)とは、データム軸直線またはデータム中心平面に関して互いに対称であるべき形体の対称位置からの狂いの大きさをいう」と定義されます。
データム平面と同一平面上に軸線や中心平面があって欲しいという形体に対して指示するものです。
加工者が何も気にせず、作業がやりやすいよう、フライス盤を使って溝や穴など加工すると対称性が崩れる可能性があります。設計意図を表すために、対称性を要求する場合はその旨を加工者に伝える必要があります。
図5に示す図面例は、円筒の中心軸が通る面をデータム平面とし、切り欠きの中心平面が、データム平面を中心として均等(±0.04)に振り分けた0.08mm離れた平行2平面の中にあれば合格品と判断されるものです。
それぞれに寸法公差が記入されていますが、独立の原則(前回参照)に従うため、寸法公差とは無関係にデータムAに対する対称度を満足させればよいということです。
位置度
JISによると、「位置度(Position)とは、データムまたはほかの形体に関連して定められた理論的に正確な位置からの点、直線形体または平面形体の狂いの大きさをいう」と定義されます。
データムを測定基準として、寸法で指示した位置にあって欲しいという形体に対して指示するもので、位置を指定する寸法を理論寸法として四角い枠で囲って表記したものと組み合わせて使用されます。
フライス盤を用いて穴位置を加工する場合、加工者の不注意がない限り、位置が大きくずれることはありませんが、一般的に図面には「フライス盤を使って加工しろ」というような指示はしません。従って、けがき線を描いてボール盤で位置を狙うような加工をされても文句はいえません。さらに、穴を開けようとする部品外形の直角や平行が出ているかどうかも分からないと、厳密な位置を規定できなくなります。設計意図を表すために、正確な位置を要求する場合はその旨を加工者に伝える必要があります。
図6に示す図面例では、ブロックのある1面をデータムAとし、それに垂直な2面をそれぞれデータムB、データムCと設定し基準を決めています。
3つの穴の中心軸がそれぞれ、理論寸法で示された狂いのない位置を中心に持つ直径0.08mmの円筒領域の中にあれば、合格品と判断されるものです。つまり、理論寸法には公差ばらつきという概念がなく、数値で示された狂いのない位置を中心として、寸法公差の代わりにどれだけ位置がずれても良いかを幾何公差値で指定するものです。
ここで、幾何公差記入枠のデータムの順序から、
「データムA」→「データムB」→「データムC」
の順に定盤や固定治具に押し当て、計測時に部品が動かないように固定するという意味を表しています。
以上、代表的な3種類の位置公差を確認しました。設計機能上どの幾何特性を指示することが最適なのか、十分理解を深めてください。
次回は4つのグループに分類される幾何特性のうち最後となる回転時の表面の振れ量を制御する「振れ公差」です。回転軸の外表面に機能を持たせる場合に必要となるものです。今回説明した同軸度や対称度と同じように、寸法ではどうやっても表現できない要素です。(次回に続く)
◎併せて読みたい「CAD」関連ホワイトペーパー:
» 主要7製品を完全網羅! 製品選定・比較に役立つ「商用3D CADカタログ 完全版」
» 【導入事例】食品加工機械メーカー不二精機による“3D CAD推進”
関連記事
 最近のJISだと「寸法公差」ではなく「サイズ公差」なのはなぜか
最近のJISだと「寸法公差」ではなく「サイズ公差」なのはなぜか
機械メーカーで3D CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。今回はJIS製図における「サイズ」「サイズ公差」「幾何公差」について考える。 「設計から製図までチャレンジしてみよう」の巻
「設計から製図までチャレンジしてみよう」の巻
図面にも触れたことのないような初心者を対象とした、図面の読み方・描き方講座。お題をクリアしながら、解説を読み進めていくことで、いつしか図面の読み描きができるようになる! 今回は、集大成として設計から製図までの一連の作業に挑戦する。 2Dと3Dの融合と、公差設計の重要性
2Dと3Dの融合と、公差設計の重要性
機械メーカーで3D CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。今回は構想設計から詳細設計までのプロセスを振り返りながら、公差設計の重要性について考える。 設計者必携! 板金設計がマスターできる絵辞書
設計者必携! 板金設計がマスターできる絵辞書
これまでの「甚さんシリーズ」の解説を少し振り返った後、この連載で使うツール「板金設計の50%がマスターできる絵辞書」を紹介する。 いまさら聞けない!? 製図の素朴な疑問たち
いまさら聞けない!? 製図の素朴な疑問たち
「外形線と寸法補助線は接して描かなければならないのか」「φは『パイ』と読むのか」などいまさら聞けない素朴な質問ばかりを集めてみた。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 有限要素法入門 〜連立方程式の解法、変位の計算〜
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- 3σと不良品発生の確率を予測する「標準正規分布表」
- ムダのない作業と楽しさをもたらす“ありそうでなかった発想”
- SUBARUが深層学習によるAI構築ツールを導入、プレス領域の成形解析工数の削減へ
- 幾何公差の基準「データム」を理解しよう
- フローで考える流れのモデリング(その2) 〜適用例と3D/1Dの関係〜
- 計算時間が従来比最大1000倍高速な流体解析ベースのトポロジー最適化ソフト
- 「設計者はなぜCAEを煙たがるのか」を考察し、広がりを阻害する壁を取り除く
- 「デザイン経営」とは? なぜデザインが経営に貢献できるのか
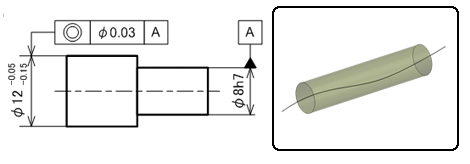 図4 同軸度の指示例と領域(面指示の場合):右側の領域を示すイラストは、データム軸線に対して同軸な円柱領域を意味します
図4 同軸度の指示例と領域(面指示の場合):右側の領域を示すイラストは、データム軸線に対して同軸な円柱領域を意味します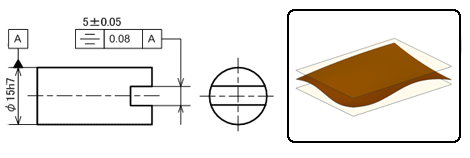 図5 対称度の指示例と領域(面指示の場合):右側の領域を示すイラストは、データム平面に対して、幾何公差分を半分ずつ均等に振り分けた平行2平面の領域を意味します
図5 対称度の指示例と領域(面指示の場合):右側の領域を示すイラストは、データム平面に対して、幾何公差分を半分ずつ均等に振り分けた平行2平面の領域を意味します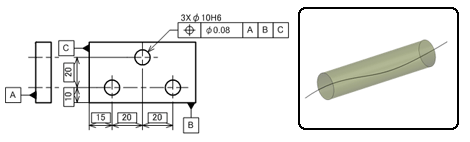 図6 位置度の指示例と領域(軸線指示の場合):右側の領域を示すイラストは、データムA、B、Cを基準として理論寸法で示された、それぞれ3カ所の位置を中心に持つ円筒領域の1つを意味します
図6 位置度の指示例と領域(軸線指示の場合):右側の領域を示すイラストは、データムA、B、Cを基準として理論寸法で示された、それぞれ3カ所の位置を中心に持つ円筒領域の1つを意味します


