回転する部品に指定する「振れ公差」:製図を極める! 幾何公差徹底攻略(9)(1/2 ページ)
同軸度と振れ公差は、どちらも同じものと勘違いしていないだろうか? 今回は、その区別をはっきりとさせよう。
今回は、4つのグループ(「形状」「姿勢」「位置」「振れ」)に分類される幾何特性のうち、最後となる部品を回転させたときの部品表面の「振れ」を規制する「振れ公差」についての解説です。
振れ公差とは
振れ公差とは、対象となる形体がデータムに関連し、回転体の表面を対象として、指定された方向の変位が偏差の許容値内にあるかを規定するものです。
姿勢公差や位置公差と同様に関連形体と呼ばれ、データムを必要とします。
振れ公差のうち、「円周振れ」は、回転させた外表面の任意の位置における部分だけを規制するものです。つまり真円度と同様に、対象部の輪切り状態を想定して、その稜線(りょうせん)のみを評価するものです。
それに対して、「全振れ」は、回転させた外表面全体をトレースして、全体に渡って規制するものです。
振れ公差の特徴として、データムとなる中心軸を中心として部品を回転させたうえで、対象部の表面のみしか指示できないことです。
振れ公差には、次の2つの幾何公差があります。
- 円周振れ(Circular run-out)
- 全振れ(Total run-out)
図1から分かるように、2つの振れ公差に上下の関係はなく、それぞれが独立して意味を持ちます。
同軸度と振れ公差はどちらも同じものと勘違いしている人が多く存在します。確かに、振れ公差もデータムに対する同軸性をうたっているように思ってしまいがちですが、これら2つの幾何公差には決定的な違いがあります。
同軸度はデータム軸線に対して対象部の中心軸線が同軸であることを規制します。振れ公差は、データム軸線を回転中心として回転させたときの対象部の外表面の振れ幅を規制するのです。
つまり、同軸度の規制する領域は「静止した円筒領域」であるのに対し、全振れ公差の規制する領域は「回転する2つの円筒のすき間」。領域が根本的に違うのです。
通常の切削加工ではあり得ませんが、円筒外周面が楕円(だえん)になって加工されると想定した場合、楕円として中心軸がデータム軸と同一であれば「同軸度=0mm」と評価されます。ところが、この部品を振れ公差で指示していれば、楕円として長径と短径の差(半径方向で0.1mm)が評価として表れることになるのです。
それでは、同軸度と振れ公差は、どのように区別して図面に指示すればよいでしょうか?
前述したように、同軸度は静的な部品に指示をします。例えば、軸受の上面をガイドローラーとして使用する場合、軸受の上面が製品の機能面になります。この機能を段付ピンだけに着目すると、板金に挿入してカシメ加工する直径がピンの位置を決める基準であり、軸受を挿入する直径が機能基準であり、同軸が要求されます。
幾何公差を使って上記の段付ピンを表す場合、板金に対して高さ方向の位置決め基準となる左側の直径をデータムAとし、軸受の高さ方向の位置を決める軸受を挿入する直径に同軸度を与えることになります。
Copyright © ITmedia, Inc. All Rights Reserved.
Special Contents
- PR -Special Contents 2
- PR -Special Site
- PR -Pickup Contents
- PR -メカ設計の記事ランキング
- 玩具から電動工具まで3月公表のリコール製品――ケガや発火の可能性も
- 3Dプリンタに注目 大阪・関西万博の見どころ【5選】
- 円筒座標系の熱伝導について考える
- 3σと不良品発生の確率を予測する「標準正規分布表」
- 幾何公差の基準「データム」を理解しよう
- CO2を回収して植物に還元する未来のベンチが万博に
- ホタテの廃棄貝殻から生まれたベンチを万博で展示 建設用3Dプリンタで製造
- ダッソーが掲げる「3D UNIV+RSES」とは? ベルナール・シャーレス氏が解説
- 富士フイルムBIの構造色インクジェット技術 万博パビリオンの建物外観に採用
- 3Dプリンタを活用し、廃プラから「大阪・関西万博」の演台/司会者台を製造

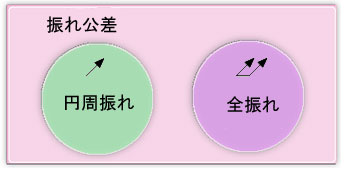 図1 振れ公差の分類
図1 振れ公差の分類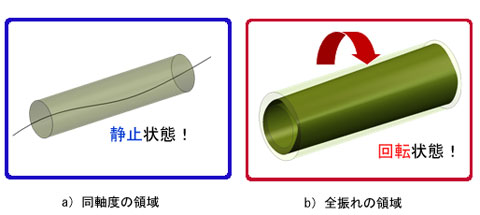 図2 同軸度と振れ公差の領域の違い 1
図2 同軸度と振れ公差の領域の違い 1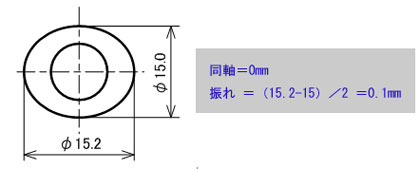 図3 同軸度と振れ公差の領域の違い 2
図3 同軸度と振れ公差の領域の違い 2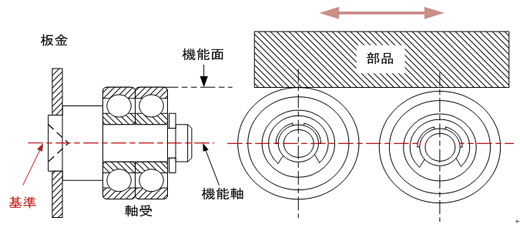 図4 同軸度を要求する構造
図4 同軸度を要求する構造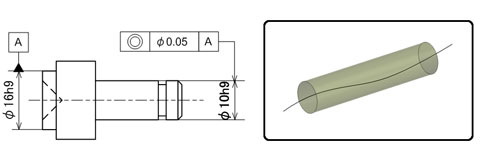 図5 同軸度を使って指示した例:右側の領域を示すイラストは、データム軸線に対して同軸な円柱領域を意味します。
図5 同軸度を使って指示した例:右側の領域を示すイラストは、データム軸線に対して同軸な円柱領域を意味します。