残存バグ数を予測する、「Gompertz曲線」による推定法とは?:山浦恒央の“くみこみ”な話(50)(1/2 ページ)
プログラマーの永遠の課題「プログラム中の残存バグ数の推定」に迫るシリーズ。第3回では、品質エンジニアが眺めているだけで“ご飯を3杯食える”ほど大好きな「Gompertz曲線」による残存バグ数の推定法を紹介する。
コーディングが終わり、コンパイルエラーも消え、いざデバッグ工程に突入――。このとき、「プログラムの中に隠れているバグの総数を正確に推定できたらなぁ……」と考えたことはありませんか? こう考えるのは何もプログラマーだけではありません。プロジェクトマネジャーも、プロジェト管理や品質制御の観点から、バグ総数を高精度で予測することを夢見ています。
――前々回は、動物学の「母数推定」を応用した、面白い発想の残存バグ数予測モデルである「キャプチャー・リキャプチャー・モデル(別名:ソフトウェア版「池の中の魚」モデル)」を紹介しました。このモデルは、“人工的にバグを埋め込む”という一種のトンデモ推定法でありました……。そして、前回、このキャプチャー・リキャプチャー・モデルの改訂版として、「『2チーム制』モデル」を解説しました。こちらは、人工バグを埋め込む必要がなく、現状の品質を維持したまま実践できる健全な方法でした。
今回は前回の予告通り、「Gompertz曲線」を使った残存バグ数の推定法を紹介します。
1.Gompertz曲線とは?
Gompertz(“ゴンペルツ”と読みます。なぜかソフトウェアの品質制御では、アルファベットで表記することが多いようです)曲線は、品質エンジニアが大好きな曲線です。
本コラムでも、第15回「最もタチの悪いバグが潜むテストフェイズとは?」、第16回「テスト消化曲線とバグ発生曲線の7パターン診断」、第17回「テストでの『ダメな猫』『普通の猫』『優秀な猫』」で取り上げました。この過去3回と少し重複しますが、ここであらためて、Gompertz曲線についておさらいしておきましょう(図1)。
例えば、「人口が増加する」「病原菌が繁殖する」「貯金を取り崩し、次第に底を突く……」など、何かが増えたり・減ったりする場合、図1のようなS字カーブを描くといわれています。ご覧の通り、はじめのうちはモタモタとしていますが、そのうち急激に増加し(あるいは減少し)、最後は頭打ちになるという、“はじめチョロチョロ、なかパッパ”的な過程をたどります。この成長、あるいは減少を表現する曲線の代表格がGompertz曲線です。今回はこれを使って、残存バグ数を予測します。
2.Gompertz曲線と数式アレルギー
Gompertz曲線を数学的に表現すると、図1の下に示した数式になります。
いかがでしょうか? この数式を見て、「えっ、何これ! さっぱり分からない……。オレには無理だぁ~」とシッポを巻いてはいけません!! 安心して良いかは別として、恐らく、世界中のソフトウェア開発エンジニアの120%が同じように思っているはずです。
筆者流に言わせてもらえば、「論理的に考えることは大好きだけど、微分、積分、三角関数、複素数みたいな解析系は大嫌い」と考える理科系人間と、「なぞなぞを解くのが大好き」という文科系人間が大集合しているのがソフトウェア業界です。ソフトウェア開発の専門書は、いわゆる理系の書籍の中で唯一、数式がほとんど出てこない珍しい分野といえるでしょう。ソフトウェア関連の本を執筆している著者が、「どうだ、これはアカデミックだろう!」と少々複雑な数式を掲載すると……、大抵その書籍は売れません。現実はそんなものです。
さて、そんな“数式アレルギー”のソフトウェア業界にあって、ただ1つ、超難解な数式が登場するのが「ソフトウェアの品質制御」です。例えば、図1の下に示したGompertz曲線の数式がそれに当たります。
ただ、こんな数式ごときにビックリする・恐れる必要はありません。ソフトウェア業界のトッププロたちは、この数式を見て次のように考えるはずです。
へぇ~。こんな複雑な指数関数の式なんだなぁ。いやぁ、お疲れさま。実際の計算式はネット上にころがってるだろうし、品質推定のパッケージになっているはずだから、それを使うことにしよう。じゃあ、次、行ってみよう!
これが、ソフトウェア開発エンジニアとしての正しい態度です。決して、“数式のジャングル”に迷い込んではいけません。
3.Gompertz曲線での残存バグ数予測
Gompertz曲線を使って、どのように残存バグ数を予測するのでしょうか? 答えは簡単で、Gompertz曲線が“どこで頭打ちになるのか”を予想すればいいのです。
プログラムのコーディングが終わり、デバッグ工程に入ると、摘出したバグの数を毎日、プロジェクトマネジャーに報告します。プロジェクトマネジャーは、全員のバグ数を集計して、バグ数の累積値をグラフにプロットします。通常、これが図1のようなGompertz曲線的なカーブになります。
残存バグ数の推測とは、「図1の『K』を推定すること」になります。
こう書くと、「何だよ! 数式不要とか言っておきながら、『K』の値を予測するには、やっぱり数式を使わなきゃならないんでしょうが!!」と不満の声が聞こえてきそうですね。実は、本当に「K」の予測にこの数式は使いません。正確に言うと「数式を使っても“意味がない”」のです。
ではなぜ、意味がないのでしょうか? 実際に、摘出バグ数をプロットしたGompertz曲線の例を図2に示します。
図2は、摘出バグ数を毎日積み上げた曲線に過ぎません。プロジェクトマネジャーは、以下のような状況で、日々のバグ摘出件数をグラフ上にプロットしています。
- デバッグ初日:1人のエンジニアが1時間デバッグして、3個のバグを見つけました
- 2日目:エンジニア3人がそれぞれ4時間デバッグして、全部で2個の不良を摘出しました
- 3日目:10人のエンジニア全員が9時間かけてデバッグして、たった3個のバグしか見つかりませんでした……
これを「人×時間」に換算すると、初日は「3人時間」、2日目は「12人時間」、3日目は「90人時間」となります。時間単位で見るとこれだけの違いがあるのに、初日、2日目、3日目と日付単位で、どんぶり勘定的にバグ摘出件数をプロットしています。ある意味、非常にいいかげんです。でも、この“いいかげんさ”が工学の神髄でもあるのです。
もしも、きちんとしたGompertz曲線を描くなら、例えば「1人時間を投入した場合の摘出バグ数」のように単位を決めて、摘出バグ数を正規化してグラフにプロットすべきです。“すべき”なのですが、以下の理由から、そんな面倒なことを実行しているプロジェクトマネジャーは、世界中のどこを探してもいないでしょう。
- デバッグするエンジニアに、「時間単位で摘出バグ数をカウントせよ!」と指示しても、面倒なので誰もやってくれない。あるいは、適当にカウントしてしまう
- プロジェクトマネジャーも、単位時間当たりの摘出バグ数をプロットするのは非常に面倒
- 摘出したバグ数は、「実際に見つけたバグ」と「それの同類をチェックして、芋づる式に見つかった類似バグ」の総和となるため、類似バグの扱いが面倒
- デバッグの基本は「疑わしきは罰する」なので、少しでもヘンな動作を見つけたらバグと見なす……。が、後で詳しく分析してみたら“実はバグではなかった”というような場合、カウントのやり直しが面倒
このように、いろいろと“面倒”なので、正確な摘出バグ数がプロットされたGompertz曲線を描くことは、実際問題として困難(ムリ)と言えます。つまり、そもそもの摘出バグ数がいいかげんなので、Gompertz曲線の数式から「K」をきちんと予測することにあまり意味がないのです。
関連キーワード
デスマーチ | 組み込み開発 | 組み込み開発プロセス改善 | 組み込み開発の混沌から抜け出そう | 現場の声からプロセス改善を深掘りする | 山浦恒央の“くみこみ”な話 | バグ | 開発プロセス | ソフトウェアテスト | システム開発
Copyright © ITmedia, Inc. All Rights Reserved.
Special Contents
- PR -Special Contents
- PR -- EDA�ス逎ッ蟠戊氛蜊��ィ�ュ髫ェ驛�ソス陷榊供蝟ァ�ス蟲ィ繝、郢晢スシ郢晢スォ邵コ�ッ邵コ�ゥ邵コ�ス竏育クコ�カ�ス貅伉ツ郢晢ソス縺倡ケァ�、郢晢スウ郢ァ蜻茨ソス陷画コ倪�陝�シア�・邵コ貅假ス∫クコ�ョ驕伜ゥ�ィ�」
- FPGA髫ェ�ュ髫ェ蛹サ竊鍋クコ鄙ォ��郢ァ險篭T4邵コ�ィLUT6邵イ竏オ�ッ遒托スシ�ス�オ蜈域」。邵コ�ォ髫穂ケ晢ス玖ォ、�ァ髢ュ�ス邵コ�ョ鬩戊シ費シ�
- 郢昜ク奇ソス郢晏ウィ縺育ケァ�ァ郢ァ�「髫ェ�ュ髫ェ蛹サ竊楢怏�ケ驍�ソス竊定ュ溽「托スサ貊督�ァ郢ァ蛛オ�らクコ貅假ス臥クコ蜷カツ竏壹&郢ァ�ケ郢晉」ッ纃セ髫戊患PGA髯ャ�ス陷ゥ竏ォ�セ�、邵コ�ィ邵コ�ッ�ス�ス
- [MONOist驍ア�ィ鬮ョ�スホ咯 驍ィ�ス竏ゥ髴趣スシ邵コ�ソ隶匁コキ蜍」陷キ莉」��郢ァ�オ郢ァ�、郢晁��ス郢ァ�サ郢ァ�ュ郢晢ス・郢晢スェ郢晢ソス縺�汞�セ驕イ謔カ�ス陷榊供鬮�坡�ソ隴滂スサ
- [MONOist驍ア�ィ鬮ョ�スホ咯 郢晢スェ郢ァ�「郢晢スォ郢ァ�ソ郢ァ�、郢晢ソスOS陋サ蠍コ�シ譏エ竏ェ邵コ�ィ郢ァ�ス�シ閧イ�ャ�ャ31陜玲ゥク�ス�ス35陜玲ゥク�シ�ス
Special Contents 1
- PR -Special Contents 2
- PR -Special Site
- PR -Pickup Contents
- PR -郢ァ�ウ郢晢スシ郢晉ソォ�ス郢晢スェ郢晢スウ郢ァ�ッ
組み込み開発の記事ランキング
- 産総研の最新スパコン「ABCI 3.0」が生成AIの研究開発と社会実装を加速する
- 米中が先行する汎用ロボット、日本がロボット大国に返り咲くには何が必要なのか
- ブレッドボードの表裏を使ってFPGA評価ボードの万能UI「dpad」を新生させる
- 45万人だけが参加できる万博のパナソニックパビリオン、半年かけた実証実験も
- 大阪・関西万博の体験型パビリオンは競争率が高過ぎてビビる
- 米国での損失は16兆円、小売店での窃盗をテクノロジーで防ぐ
- ネットワーク不要で産業機器の故障予兆検知ができるAI機能搭載マイコン
- 車載マイコンで快走のインフィニオン、なぜRISC-Vを採用するのか
- CAN通信におけるデータ送信の仕組みとは?
- CANプロトコルを理解するための基礎知識

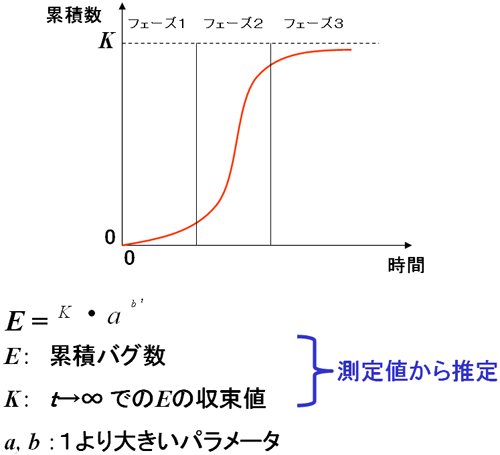 図1 Gompertz曲線 ※第15回の図1を再掲
図1 Gompertz曲線 ※第15回の図1を再掲
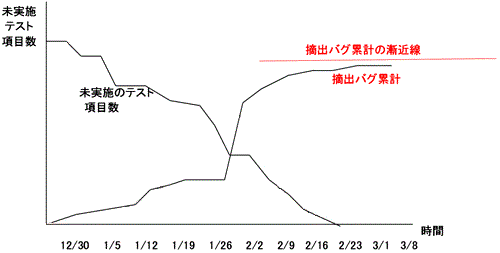 図2 デバッグでのGompertz曲線
図2 デバッグでのGompertz曲線