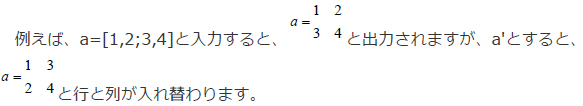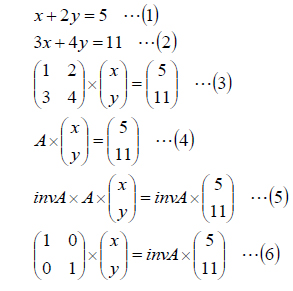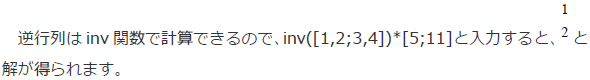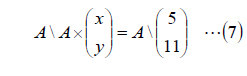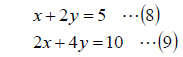固有値問題を用いて応力計算してみよう:無償ソフトで技術計算しよう【入門編】(4)(1/2 ページ)
FreeMatの基本を一通り覚えたら、固有値問題を用いて応力計算の例題を解いてみよう。
「そうか、FreeMatとは『自由に寝転べる場所』という意味ではなく、行列を扱えるフリーソフトだったのか!」……などという冗談はさておいて……、今回は配列の操作について説明します。
筆者注:FreeMatはコマンド入力後にエンターキーを押すとコマンドを実行します。本連載ではエンターキーの記述を省略しますが、操作の際にはコマンド入力後にエンターキーが必要です。
配列の生成
配列への入力は[ ]内に数値をカンマやセミコロンでつないで配置しますが、連続した数値などはコマンドでの入力が可能です。
A:B:Cと入力すると、Aから始まり、CまでBずつ増加する配列が得られます。例えば、1:1:10とすると、「1 2 3 4 5 6 7 8 9 10」と出力されます。増分が1の場合は1:10のように、省略可能です。
同じような方法ですが、linspace(A,B,C)と入力すると、AからBの間にCだけ等間隔に数値を生成します。例えば、linspace(1,10,10)とすると、「1 2 3 4 5 6 7 8 9 10」と出力されます。Cは生成される数値の数であり、分割数はC−1となることに注意してください。Cを省略することも可能で、省略した場合、C=100と見なして100個の数値を作り出します。
logspace(A,B,C)とすると、10^Aから10^Bの間に対数スケールで等間隔にCだけ数値を生成します。
要素が0だけの配列を生成するにはzeros(m,n)とします。zeros(m,n)では、0がm行n列並んだ配列を生成します。一方、要素が1だけの配列を生成するにはones(m,n)とします。ones(m,n)では、1がm行n列並んだ配列を生成します。正方行列の場合、zeros(m)あるいはones(m)と入力するだけでm行m列の配列を生成します。m行m列の単位行列を生成するには、eye(m)とします。
要素を含まない空配列は[ ]とします。空配列は後述するように、要素を削除する場合に用います。
配列の操作
次に配列の操作について説明します。
配列をつなげる場合、横方向にはカンマ,でつなぎ、また、縦方向にはセミコロンでつなぎ、[ ]で囲みます。例えば、a=[1,2,3];b=[4,5,6];と入力し、[a,b]とすると、「1 2 3 4 5 6」と1行6列の配列となります。
特定の要素の書き換えは、配列(行、列)=数値とします。例えば、a=[1,2;3,4]と入力し、a(2,2)=1とすると、2行2列目の4が1に置き換わります。数値の代わりに、空配列[ ]を用いると、要素を削除することができます。例えば、a=[1,2,3,4]と入力して、a(1)=[ ]とすると、aは「2 3 4」となり、先頭の1が削除され、それぞれの要素は前に移動し、aは1行3列の配列となります。配列は矩形となっていなければならないので、m行n列の配列で削除する場合は、行全体あるいは列全体を指定します。例えばa=[1,2;3,4]で、1行目を削除するにはa(1,:)=[ ]とします。また、1列目を削除するには、a(:,1)=[ ]とします。
配列の行数、列数を調べるには、size(配列)とします。例えば、size(zeros(4,5))と入力すると、4,5と行、列の順に出力されます。出力された行数、列数を変数として利用するには、[r,c]=size(zeros(4,5));と入力します。rには行数が、cには列数が格納されます(r、cはxやyとしても構いません)。
length(配列)とすると、行数、列数のうち、大きい方の数値を返します。例えば、length(zeros(4,5))と入力すると、5と出力されます。
転置(行と列を入れ替える)は、右側に「'」(シングルクォーテーション)を入れます。
flipud,fliplrはそれぞれ、配列を上下反転、左右反転させます。
reshape(x,m,n)は配列xをm行n列に並べ替えてくれます。この際、並べ替えの順序は1列目上から下、2列目上から下〜の順番で並んだ数値を並べ替えます。
flipdimは配列の列方向や行方向を反転させます。flipdim(配列,1)とすると、行方向を反転させ、flipdim(配列,2)とすると、列方向を反転させます。
要素を昇順に並べ替えるにはsortを用います。ここで、ソートの例題用データを作成する際に便利なrandperm関数も紹介します。randperm(n)と入力すると、1〜nまでの自然数をランダムシャッフルした配列を出力します。例えば、a=randperm(5);とすると、aには、「2,4,1,5,3」という配列が入力されます(ランダムシャッフルなのでこのならびになるとは限りません)。sort(a)と入力すると、「1,2,3,4,5」と昇順に並び替えた配列を出力します。
特定の条件に一致した要素を書き換えるには、論理演算とfind関数を組み合わせます。例えば、先ほどの変数a=[2,4,1,5,3]で、3より大きい要素は0に置き換えるには、a(find(a>3))=0と入力します。すると、「2 0 1 0 3」と4と5が0で置き換わった配列となります。動作を説明すると、論理演算a>3では、a>3を満足する要素は1、満足しない要素は0を出力します。つまり、「0 1 0 1 0」を出力します。findは1の要素の場所を出力します。この場合、2と4になります。要素の場所をaに指示し、0を格納することで、目的の要素が0に置き換わります。
diag(配列)は、対角要素を取り出します。tril(配列)は、対角要素を含んだ下三角に並んだ要素以外を0にします。また、triu(配列)は、対角要素を含んだ上三角に並んだ要素以外を0にします。
配列の操作は、配列の内部を確認しないと結果が分からないため、大規模な配列操作を行う場合は、小さな配列で動作を確認しておくことをおすすめします。
文字列
文字列は文字の配列として扱われます。c='FreeMat';(文字列は「'」で囲みます)と入力し、c(1)と入力すると、先頭の文字Fが出力されます。文字列をつなげる場合、配列をつなげるのと同じで、['Hello! ','FreeMat']のように、カンマ,でつなぎ[ ]で囲みます。
セル配列
配列は、数値や文字を混在させることはできません。これに対して、セル配列は、数値、文字や数値配列、文字列を配列とすることができます。セル配列を入力するには、{ }で囲みます。例えば、{1,[2,3],'a','FreeMat'}と入力すると、[1] [1x2 double array] [a] [FreeMat]と出力されます。セル配列から要素を取り出すには、{行、列}と指定します。先ほどの入力内容は変数ansに入っているので、例えば、ans{1,2}と入力すると、2列目にある数値配列の要素2,3が出力されます。
逆行列、バックスラッシュ演算
FreeMatを使うと連立方程式が簡単に解けます。例えば、(1)(2)式は(3)式のような行列の積で表せます。このうち、係数行列をAとして、(4)式のように表して、(5)式に示すように逆行列invAを両辺に掛けると、(6)式のように、左辺は単位行列とxyベクトルとの積になり、右辺に解が求まります。
この一連の操作は、(7)式のように両辺を係数行列Aで左側から割っているとも考えられます。
左側から割る操作はバックスラッシュ演算と呼ばれ、\あるいは\を使います(キーボード上の\はフォントによっては、\と表示されます)。
一般に上述のようにして答えが得られるのは、行列式が0ではないという前提条件が必要となります。例えば、下の(9)式は(8)式の両辺を2倍したもので、両式は同じであるため、(8)(9)の連立方程式は解けません。この場合、det([1,2;2,4])として行列式を計算すると、0となります。一般に、あらかじめ行列式を計算して、0ではないことを確認してから連立方程式を解きますが、FreeMatは、方程式を解く際に行列式が0だと警告してくれるので、前もって行列式を計算する必要はありません。
試しに、[1,2;2,4]\[5;10]と入力して、(8)(9)式を解いてみると、下記のような警告が表示され、行列式が0となっている可能性があることが分かります。
Warning: Matrix is singular to working precision.
「単一の行列となっているため正しく計算できない」という意味です。
2元以上の多元連立方程式を解く場合も同じで、右辺を係数行列でバックラッシュ演算すれば、解が得られます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 有限要素法入門 〜連立方程式の解法、変位の計算〜
- 3σと不良品発生の確率を予測する「標準正規分布表」
- SUBARUが深層学習によるAI構築ツールを導入、プレス領域の成形解析工数の削減へ
- ムダのない作業と楽しさをもたらす“ありそうでなかった発想”
- パナソニックが再生家電を売る理由、サーキュラーエコノミーだけが目的ではない
- 「設計者はなぜCAEを煙たがるのか」を考察し、広がりを阻害する壁を取り除く
- 幾何公差の基準「データム」を理解しよう
- 「デザイン経営」とは? なぜデザインが経営に貢献できるのか
- ARで掃除した経路をリアルタイムで可視化、ダイソンが無駄のない掃除体験を提案
- 計算時間が従来比最大1000倍高速な流体解析ベースのトポロジー最適化ソフト