曲面と曲線、2種類の3次元グラフの描き方:無償ソフトで技術計算しよう【グラフィックス編】(3)(1/2 ページ)
今回は、FreeMatによる3次元グラフ作成についての解説となる。「曲線表示」と「曲面表示」の2種類について説明する。
前回は、対数スケールでのプロットや、タイトルやラベルの追加、スケールの変更などのグラフの修飾に関するコマンドについて説明しました。今回は、3次元のグラフを表示する方法について説明します。3次元グラフには「曲線表示」と「曲面表示」の2種類があります。曲線表示、視点の変更、曲面表示の順に説明します。
筆者注:FreeMatはコマンド入力後にエンターキーを押すとコマンドを実行します。本連載ではエンターキーの記述を省略しますが、操作の際にはコマンド入力後にエンターキーが必要です。
3次元曲線プロット
曲線表示は2次元プロットと同じ要領で作成できます。具体的には「plot3(x座標,y座標,z座標)」と入力します。例として、1回転当たり1上昇するらせん曲線を描いてみます。
d=0:360*3;plot3(cosd(d),sind(d),d/360); view(3)と入力すると、図1が得られます。view(3)は視点を変えるコマンドで、詳しくは次項で説明します。
もう1つ例題を説明します。減衰系の強制振動での振幅倍率曲線は以下の式で表されます。
ここで、x/xstは静荷重での変位xstに対する振幅x、η=f/fnは共振周波数fnに対する周波数f、ζは減衰比を表します。振動の周波数が共振周波数に近づくほど振幅は増大し、減衰比ζが小さいほど振幅は急速に増大します。これをグラフ化するのが下記のex203.mというプログラムで、図2が得られます。
clear;
eta=0:0.01:3;
zeta=[0.1,0.25,0.5,1];
hold('on');
for n=1:length(zeta)
mf=1./sqrt((1-eta.^2).^2+(2*zeta(n)*eta).^2);
plot(eta,mf);
end
xlabel('f/fn');ylabel('x/xst');grid('on');
図2は振動工学の本には良く見かける図ですが、プロットにコメントがないと、それぞれの曲線がどのζに対応しているのか分かりにくいのが難点です。これを立体的なグラフを描くように改造したものがex204.mです。
ex204.mでは、プロットコマンドとして、plot3を使い、y座標としてζの値を使います。
clear;
eta=0:0.01:3;
zeta=[0.1,0.25,0.5,1];
hold('on');
for n=1:length(zeta)
mf=1./sqrt((1-eta.^2).^2+(2*zeta(n)*eta).^2);
plot3(eta,zeta(n)*ones(1,length(eta)),mf);
end
xlabel('f/fn');ylabel('zeta');zlabel('x/xst')
grid('on');view(3);
この際、x座標、z座標と要素数を合わせる必要があるため、zeta(n)*ones(1,length(eta))として、要素が1で要素数がetaと同じ数の配列にzetaを掛けたものをy座標としています。この結果、得られたのが図3で、図2と比べて、ζの変化に対する振幅倍率の変化が分かりやすくなっています。
このように、FreeMatでは、わずかな手間でグラフを立体的に表現することが可能です。
視点の変更
3次元グラフでは視点の向きにより、見やすさが変わります。そこで、視点を変更する方法について説明します。視点を変更するには2つ方法があります。1つは、グラフウィンドウの右から3番目の円すい形のRotateアイコンをクリックし、グラフ上でマウスを左ドラッグする方法です。もう1つは、viewコマンドを用います。
viewコマンドについてのヘルプが下記です。
The view function sets the view into the current plot. The simplest form is view(n)
where n=2 sets a standard view (azimuth 0 and elevation 90), and n=3 sets a standard 3D view (azimuth 37.5 and elevation 30).
With two arguments, view(az,el) you set the viewpoint to azimuth az and elevation el.
viewは現在のプロットの視点を設定します。view(n)という記述では、n=2だと、方位角が0度で迎え角が90度になり、n=3だと、方位角が37.5度で迎え角が30度に設定されます。view(az,el)という記述では、方位角をazで、迎え角をelで指定します。
図1や図3を描く際に使われたview(3)というコマンドは、方位角37.5度、迎え角30度の方向から見るようにグラフを設定していることになります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 有限要素法入門 〜連立方程式の解法、変位の計算〜
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- 3σと不良品発生の確率を予測する「標準正規分布表」
- ムダのない作業と楽しさをもたらす“ありそうでなかった発想”
- SUBARUが深層学習によるAI構築ツールを導入、プレス領域の成形解析工数の削減へ
- 幾何公差の基準「データム」を理解しよう
- フローで考える流れのモデリング(その2) 〜適用例と3D/1Dの関係〜
- 計算時間が従来比最大1000倍高速な流体解析ベースのトポロジー最適化ソフト
- 「設計者はなぜCAEを煙たがるのか」を考察し、広がりを阻害する壁を取り除く
- 「デザイン経営」とは? なぜデザインが経営に貢献できるのか
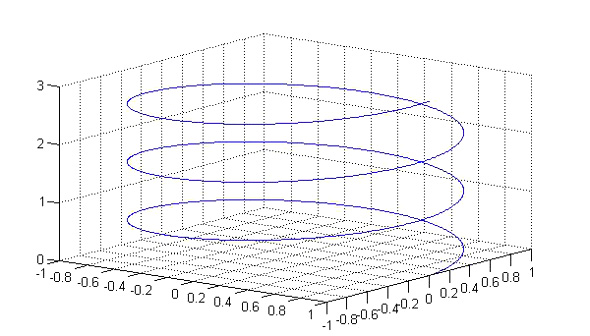 図1 らせん曲線
図1 らせん曲線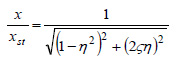
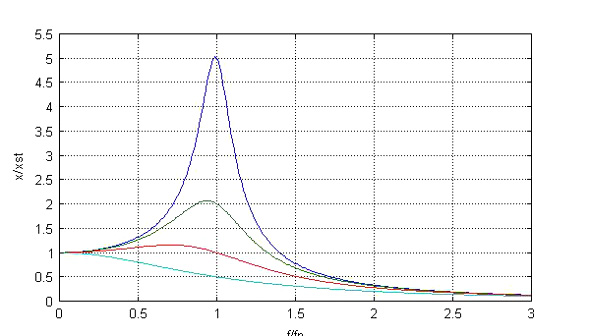 図2 振幅倍率曲線 2次元プロット
図2 振幅倍率曲線 2次元プロット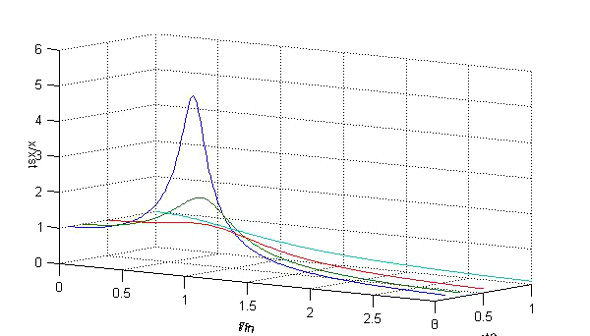 図3 振幅倍率曲線 3次元プロット
図3 振幅倍率曲線 3次元プロット

