再帰アルゴリズムで「ハノイの塔」のプログラムを書く:無償ソフトで技術計算しよう【プログラミング処理編】(3)(1/2 ページ)
「再帰」とは、「自分で自分を呼び出す」ようなアルゴリズム。再帰アルゴリズムを使うと、有名なパズル「ハノイの塔」のプログラムがシンプルに書ける。
前回は、基本的アルゴリズムに対応するコマンドについて解説しました。今回は「再帰アルゴリズム」について説明します。かつてプログラミングに挫折した方は、ここで、もう一度がんばってみてください。……これは「再起」でしたね。
再帰アルゴリズムの「再帰」とは、「自分で自分を呼び出す」ようなアルゴリズムのことで、これをうまく使うととても簡単に問題を解くことが可能です。
筆者注:FreeMatはコマンド入力後にエンターキーを押すとコマンドを実行します。本連載ではエンターキーの記述を省略しますが、操作の際にはコマンド入力後にエンターキーが必要です。
再帰アルゴリズム
再帰とは、自分を呼び出す処理で、再帰アルゴリズムでは、関数mファイルの中で自分自身を呼び出します。例を基に説明します。
フィボナッチ数とは、下記の式で定義される数です(関連記事:forやwhileで繰り返し処理させてみる)。
これをそのまま、プログラムに書き出すと、「ex318.m」の再帰アルゴリズムによるフィボナッチ数の計算プログラムができます。
function fi=ex318(k)
if(k<=2)
fi=1;
else
fi=ex318(k-1)+ex318(k-2);
end
ただし、フィボナッチ数は下記の「ex319.m」のように、forループでも求めることが可能で、一般にforループで作成できるような問題には、再帰アルゴリズムは適していません。
function fi=ex319(k)
f=zeros(1,k);
f(1)=1;f(2)=1;
for n=3:k
f(n)=f(n-1)+f(n-2);
end
fi=f(k);
試しに、両者の計算時間をtic、tocコマンドで計測してみると、下記のように、再帰アルゴリズムを用いた「ex318.m」では、0.009秒に対して、漸化式をforループで計算した「ex319.m」では、0.001秒と再帰アルゴリズムを使わない方が計算効率が良くなります。これは、再帰アルゴリズムでは何度もプログラムを呼び出すためです。
--> tic;ex318(10);time=toc time = 0.0090 --> tic;ex319(10);time=toc time = 0.0010
再帰アルゴリズムは、簡単に言うと、人に優しく、コンピュータに厳しいアルゴリズムです。従って、フィボナッチ数の計算のように、簡単な問題では、コンピュータに厳しいだけの結果となります。では、次に、再帰アルゴリズムの代表的な問題であるハノイの塔の問題で、どのくらい「人に優しいか」を説明します。
再帰アルゴリズムによるハノイの塔の解法
ハノイの塔とは、パズルの一種で、図1のように3本の棒と大きさの異なる穴あき円盤からなり、「円盤を1回に1枚ずつ移動できるが、小さな円盤の上に大きな円盤を載せることはできない」というルールに従い、全ての円盤を中央の棒に移動させるというものです。
例えば、円盤が2枚の場合、一番上の円盤を右端の棒に移動させ、残った円盤を中央の棒に移動させ、右端の棒の円盤を中央の棒に移動させれば、全ての円盤が中央の棒に移動します。ところが、円盤が3枚以上となると途端に難しくなります。これを再帰アルゴリズムで解いてみます。
はじめに、左端の棒をfrom、中央の棒をto、右端の棒をworkと名付けます。左端の棒にはn枚の円盤が載っているとします。どうやってやるかは問わないとして、n枚の円盤を左端の棒から中央の棒に移動させる操作を、hanoi(n,from,to,work)と名付けます。hanoi(n,from,to,work)は1番目の引数つまりn段を2番目の引数から3番目の引数に移動させるという意味です。
図2を見ると分かるように、ちょっとルールを無視して、上からn-1段目までを右端の棒に移動させ、残ったn段目の円盤を中央の棒に移動させ、先ほど移動したn-1段目までを右端の棒から中央の棒に移動させれば、完成します。
上からn-1段目までを右端の棒に移動させる操作は、hanoi(n-1,from,work,to)となります。hanoi(n-1,from,work,to)は、n-1段分をfromからworkに移動させよという意味です。
残ったn段目の円盤の移動は自分で行うとして、「n段目の円盤をfromからtoに移動させよ」と表示します。
移動したn-1段目までを右端の棒から中央の棒に移動させる操作は、hanoi(n-1,work,to,from)となります。hanoi(n-1,work,to,from)はn-1段分をworkからtoに移動させよという意味です。以上の操作を円盤が最後の1枚になるまで繰り返せばよいことになります。
プログラムにすると、下記のようになります。驚くほどシンプルです。実行させるにはコマンドウィンドウで「hanoi」(段数,左端の棒の名前,中央の棒の名前,右端の棒の名前)と入力します。
function hanoi(n,from,to,work)
if(n>0)
hanoi(n-1,from,work,to);
disp(['move the ',num2str(n),'th disk from ',from,' to ',to]);
hanoi(n-1,work,to,from);
end
コマンドウィンドウで、hanoi(3,'Left','Center','Right')とすると、下記のように円盤の移動方法を表示します。得られた移動方法を基に移動途中の円盤の状態を図にしたものが図3です。確かに、3枚の円盤が中央の棒に移動することが分かります。このように再帰アルゴリズムを用いると、複雑な問題の解法もシンプルに記載できます。ハノイの塔の解法は、再帰アルゴリズムの代表的な例題です。
move the 1th disk from Left to Center move the 2th disk from Left to Right move the 1th disk from Center to Right move the 3th disk from Left to Center move the 1th disk from Right to Left move the 2th disk from Right to Center move the 1th disk from Left to Center
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 知らないと取り返しがつかなくなる金型の費用と作製期間の話
- 3σと不良品発生の確率を予測する「標準正規分布表」
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- 幾何公差の基準「データム」を理解しよう
- 3D機構検証ソフトの最新版、干渉検証漏れ防止機能を搭載
- Excelを使って周波数分析をやってみよう!
- 「データム記号」の使い方と設計者が身に付けておくべき作法
- ムダのない作業と楽しさをもたらす“ありそうでなかった発想”
- AI活用機能を強化した「AutoCAD 2025」「AutoCAD Plus 2025」をリリース
- 位置度を考える上で重要な「最大実体公差」
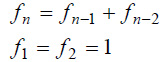
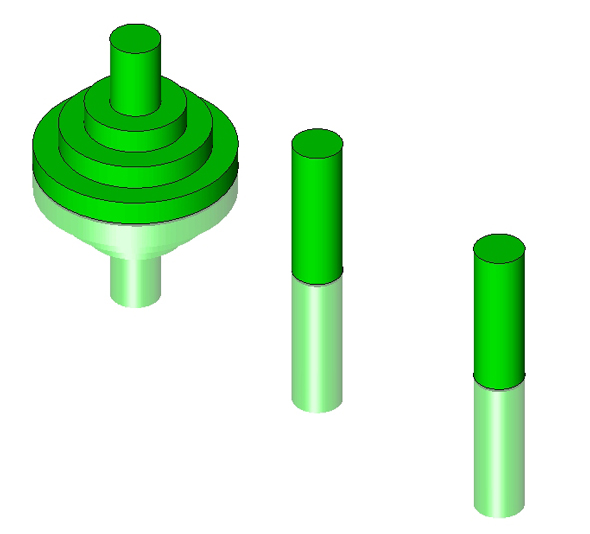 図1 ハノイの塔
図1 ハノイの塔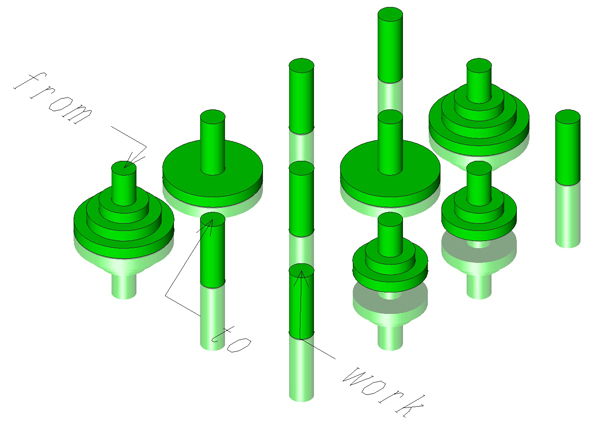 図2 n-1段目の移動
図2 n-1段目の移動 図3 3枚の円盤の移動
図3 3枚の円盤の移動

