振動問題をFreeMatで解いてみよう(その1):無償ソフトで技術計算しよう【シミュレーション応用編】(2)(1/3 ページ)
今回は振り子の運動方程式や減衰振動を無償ソフト「FreeMat」で解いてみる。
» 2015年03月19日 10時00分 公開
[伊藤孝宏,MONOist]
今回と次回の2回にわたって振動問題をFreeMatで解く方法を説明します。
振り子の振動
振動問題の基本となる振り子について、運動方程式を導いてみます。図1に示す振り子の軌道に沿ってx座標を取ると、運動方程式は以下のようになります。
振り子の長さLと振れ角θとの関係から、x=L・θを用いると下記となります。
振り子の振れ角が小さい場合、sinθ≅θと見なせるので、(1)式は下記となります。
(2)式の一般解は、下記となります。
初期条件を例えば、t=0で、
として係数AとBを求めると下記となります。
周期は下記のとおりの振動となります。
以上は、振れ角が小さい場合には成り立ちますが、振れ角が大きくなると、sinθ≅θとは見なせなくなるので、下記の式を解く必要があります。
(1)式を解析的に解くことは大変な作業になるので、数値的に解いてみます。ちなみに、シミュレーション編の冒頭で紹介した図は、(1)式を数値的に解いたものです。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 3σと不良品発生の確率を予測する「標準正規分布表」
- 知らないと取り返しがつかなくなる金型の費用と作製期間の話
- 若手エンジニアにありがちな強度設計ミス【前編】
- 幾何公差の基準「データム」を理解しよう
- Excelを使って周波数分析をやってみよう!
- AI活用機能を強化した「AutoCAD 2025」「AutoCAD Plus 2025」をリリース
- 「データム記号」の使い方と設計者が身に付けておくべき作法
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- 位置度を考える上で重要な「最大実体公差」
- FreeCADってどんな3D CAD? 簡単なモデリングから始めてみよう
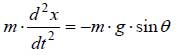
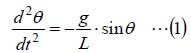
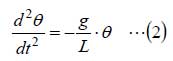
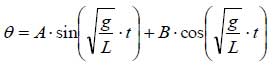
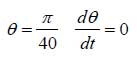
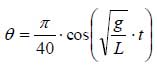
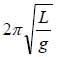
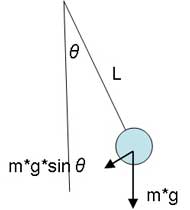 図1:振り子
図1:振り子


