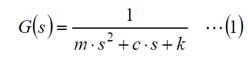ボード線図を使って過渡応答と周波数応答を求める:無償ソフトで技術計算しよう【制御工学応用編】(1)(1/3 ページ)
【制御工学応用編】では、制御系の応答性や安定性を評価する方法とPIDコントローラーの設計について説明する。今回は、過渡応答と周波数応答について取り上げる。
| FreeMatでエンジニアリング計算: | |
|---|---|
| ⇒ | 入門編 |
| ⇒ | グラフィックス編 |
| ⇒ | プログラミング基礎編 |
| ⇒ | プログラミング処理編 |
| ⇒ | プログラミング応用編 |
| ⇒ | シミュレーション基礎編 |
| ⇒ | シミュレーション応用編 |
| ⇒ | 制御工学基礎編 |
【制御工学応用編】では、制御系の応答性や安定性を評価する方法とPIDコントローラーの設計について説明します。今回は、過渡応答と周波数応答について説明します。
過渡応答と周波数応答
図1はバネ・マス・ダンパ系で、図2は図1の系に周波数0.5Hzと1Hzで周期的に変動する荷重を与えた場合の変位を示したものです。
下記のex506.mで計算しています。詳しくは【シミュレーション応用編】(3)をご覧ください。
clear;c=1;k=10;m=1;fr=[0.5,1];
for n=1:2
dydt=@(t,y) [y(2);(sin(fr(n)*2*pi*t)-c*y(2)-k*y(1))/m];
[t,y]=ode45(dydt,[0,20],[0;0]);
subplot(2,1,n);plot(t,y(:,1));grid('on');
xlabel(['Frequency=',num2str(fr(n)),'[Hz]']);
ylabel('Height[m]');ylim([-0.4,0.4]);
end
図2を見ると、最初の変動の後は、一定の変動となることが分かります。例えば、図2下段の1Hzでの変位は、最初は大きく、その後は規則正しい変動となっています。この最初の変動が自由応答と呼ばれ、システムの初期値や特性(この場合、m、c、kや初期変位など)に依存します。自由応答の特性を調べるのが過渡応答です。過渡応答には、幾つか種類がありますが、ここでは、インパルス応答について説明します。一方の自由応答の後の規則正しい変動は、強制応答と呼ばれ、強制力(この場合、周期的荷重)に依存します。強制応答の特性を調べるのが周波数応答です。
さて、図2で強制応答の振幅に注目すると、荷重の周波数により異なることが分かります。また、周波数が2倍の関係にあるにも関わらず、振幅の山と谷の位置がずれていることも分かります。このように、強制応答は与えられた強制力の周波数により、振幅や位相が変化します。周波数の変化に対する応答を調べるため、強制応答の特性については「周波数応答」と呼ばれています。では、図1に示すバネ・マス・ダンパ系を例に、インパルス応答、周波数応答を求めてみます。参考に、図1のバネ・マス・ダンパ系の伝達関数を下記に示します。
伝達関数とその求め方は【制御工学基礎編】(2)を参照してください。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- 有限要素法入門 〜連立方程式の解法、変位の計算〜
- 3σと不良品発生の確率を予測する「標準正規分布表」
- ムダのない作業と楽しさをもたらす“ありそうでなかった発想”
- 知らないと取り返しがつかなくなる金型の費用と作製期間の話
- SUBARUが深層学習によるAI構築ツールを導入、プレス領域の成形解析工数の削減へ
- 幾何公差の基準「データム」を理解しよう
- フローで考える流れのモデリング(その2) 〜適用例と3D/1Dの関係〜
- 計算時間が従来比最大1000倍高速な流体解析ベースのトポロジー最適化ソフト
- 「設計者はなぜCAEを煙たがるのか」を考察し、広がりを阻害する壁を取り除く
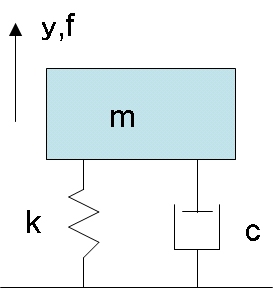 図1:バネ・マス・ダンパ系
図1:バネ・マス・ダンパ系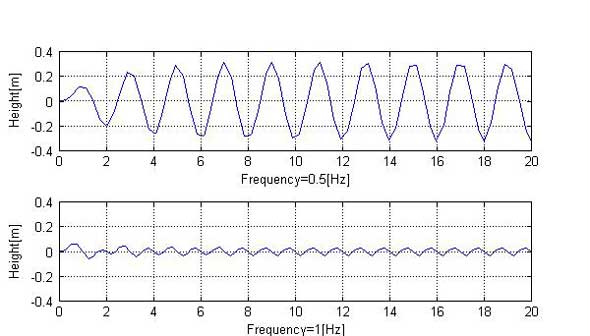 図2:バネ・マス・ダンパ系の周期的加振に対する応答
図2:バネ・マス・ダンパ系の周期的加振に対する応答