制御系が暴走しないように設計する:無償ソフトで技術計算しよう【制御工学応用編】(2)(1/2 ページ)
【制御工学応用編】では、制御系の応答性や安定性を評価する方法とPIDコントローラーの設計について説明する。今回はFreeMatを使って、制御系の安定・不安定の状態を判別してみる。
制御系の安定性
今回は、制御系の安定性を判定する方法について説明します。制御系に要求されることは、第一に「暴走しないこと」です。「暴走しない」、すなわち「出力が発散しない」という性質が「安定性」です。従って、制御系の設計では、安定性を判別することが重要になります。
【制御工学基礎編】(3)のPIDコントローラー付バネ・マス・ダンパ系を例に、出力が暴走する様子を見てみます。図1がPIDコントローラー付バネ・マス・ダンパ系のブロック線図で、制御目標値を0.1とした場合の出力をex510.mで求めます。
clear;m=1;c=1;k=10;ki=10;kd=10;yset=0.1;kp=[10,-9.09,-10];
for n=1:3
dydt=@(t,y) [y(2);(-(c+kd)*y(2)-(k+kp(n))*y(1)+kp(n)*yset+y(3))/m;ki*(yset-y(1))];
[t,y]=ode45(dydt,[0,50],[0;0;0]);
subplot(1,3,n);plot(t,y(:,1));grid('on');
title(['kp=',num2str(kp(n))]);xlabel('Time[s]');ylabel('Height[m]');
end
詳しくは【制御工学基礎編】(3)を参照してください。
比例定数kpを10、-9.09、-10とした場合の出力を図2に示します。Kp=10では、出力は目標値0.1に収束しています。このように、出力が一定値に収束するものを安定と呼びます。一方、kp=-10では、出力は振動しながら振幅が増大し続けます。このように、出力が収束することなく発散するものを不安定と呼びます。また、Kp=-9.09では、出力が振動し続けます。これは、収束も発散もしない状態であるため、安定限界と呼ばれます。
今回は安定・不安定の状態を見るために、FreeMatで出力を求めましたが、出力が安定するかどうかを調べるだけであれば、伝達関数から求めることが可能です。次に、伝達関数から出力の安定性を判定する方法について説明します。
伝達関数の極と安定性
図1のブロック線図の伝達関数を下記に示します。ブロック線図から伝達関数を求める方法については【制御工学基礎編】(3)を参照してください。
(1)式で分母D(s)は「特性多項式」と呼ばれます。Dは「Denominator」(分母)の略で、Nは「Numerator」(分子)の略です。また、D(s)=0は「特性方程式」と呼ばれ、特性方程式の解、すなわちD(s)=0を満たすsは「極」と呼ばれます。特性方程式の解は一般に複素数となります。複素数とは実数と虚数の和で示される数値です。ちなみに、N(s)=0の解は「零点」と呼ばれます。
結論から言えば、極、すなわち特性方程式の解が正の実数部を持つと不安定になります。つまり、D(s)=0を解いて、sの実部が正か負かを調べればよく、実部が全て負であれば安定です。また、実部が0の極が存在すると、出力は振動し続け、安定限界となります。
簡単に言いましたが、高次多項式の解を求めることは簡単ではありません。そのため、ラウス・フルビッツなどの特性方程式を解かずに安定性を判別する各種の方法が提唱されています。ただ、FreeMatを使えば、高次多項式を数値的に解くことが可能です。そこで、ここでは特性方程式を解いて安定・不安定の判定を行ってみます。
具体的には、多項式の高次の項から順に係数を配列としてrootsコマンドに渡せば、解が求まります。例えば、S3+11s2+10=0であれば、多項式の係数は高次の項から[1,11,0,10]であるため、
--> roots([1,11,0,10])
と入力すると、
ans = -11.0814+0.0000i 0.0407+0.9491i 0.0407-0.9491i
のように解が求まります。
ただし、
のように、分子も同じ解を持つと、s=1という極は零点と相殺されます。そこで、D(s)=0とN(s)=0を解いた解をプロットして、両者が重ならないことも確認することにします。
具体的には、図2の発散するケースの伝達関数では、
--> plot(roots([1,11,0,10]),'o',roots([10,-10,10]),'x')
として、図3をプロットします。
図3は横軸が実数、縦軸が虚数で、「○」がD(s)=0の解、すなわち極で、「×」がN(s)=0の解、すなわち零点です。図3を見ると、実数部が正の箇所に「○」が2か所あり、かつ「×」とは重ならないため、不安定となることが分かります。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 3σと不良品発生の確率を予測する「標準正規分布表」
- 知らないと取り返しがつかなくなる金型の費用と作製期間の話
- 若手エンジニアにありがちな強度設計ミス【前編】
- 幾何公差の基準「データム」を理解しよう
- Excelを使って周波数分析をやってみよう!
- AI活用機能を強化した「AutoCAD 2025」「AutoCAD Plus 2025」をリリース
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- 「データム記号」の使い方と設計者が身に付けておくべき作法
- 位置度を考える上で重要な「最大実体公差」
- FreeCADってどんな3D CAD? 簡単なモデリングから始めてみよう
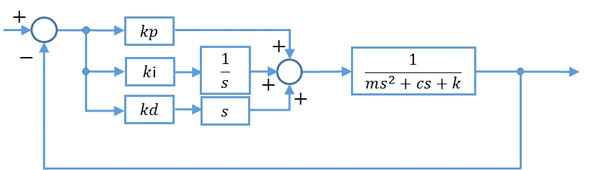 図1:PIDコントローラー付バネ・マス・ダンパ系
図1:PIDコントローラー付バネ・マス・ダンパ系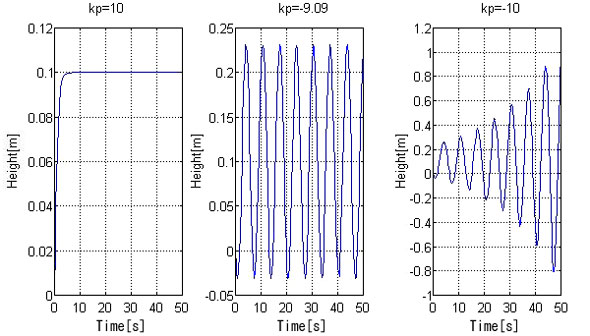 図2:比例定数の安定性への影響
図2:比例定数の安定性への影響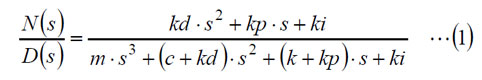
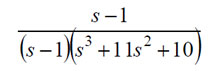
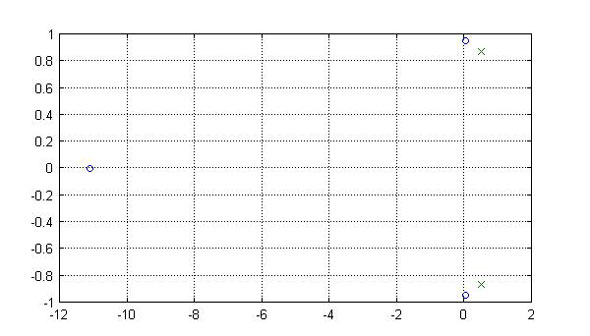 図3:極配置「○」と零点配置「×」
図3:極配置「○」と零点配置「×」

