モデリングはなぜ失敗するのか―― 悪いモデル、汚いモデル、意味がないモデル:プロジェクトを成功させるモデリングの極意(4)(1/10 ページ)
誰もが失敗したくてモデリングする訳ではないのに、失敗しているモデリングを見る機会は減りません。今回はモデルの失敗例を通じてその原因を探ります。
「モデリングはなぜ失敗するのか」――今回はモデリングが失敗する原因を探っていきましょう。誰しもが失敗したくてモデリングをしているわけではありません。しかしモデリングが失敗している例を多く見かけます。
どこがいけなかったのか、何が悪かったのか、なぜ私たちはモデリングに失敗したのか。今回はモデリングで失敗する原因を見つけていき、これらの失敗から学んでいくようにします。
はじめに
連載の第1回と第2回ではモデリングの目的や手法、ツールを見てきました。前回の第3回ではUMLやSysMLの使いにくいところとその対処法、そしてモデリングの分類や工程別のモデリング、アジャイル開発などとの関係を見てきました。その中でも失敗する例と原因を幾つか紹介しました。今回はそれらも含めて失敗の例と、それが起こった状況やその原因を見ていきます。
そしてこの失敗から、直接の原因と真の原因を探っていきます。このために「なぜなぜ分析」を2段階程度やってみて、真の原因を探ります。なお、なぜなぜ分析を3段階以上してしまうと、社会が悪い、会社が悪い、自分が悪い、生きていていいですかというような極論的な結論が出そうなので、なぜなぜ分析は2段階ぐらいが適当です。今回はその内の1段階目の直接的な原因を紹介します。さらに次の段階は次回に掲載する予定です。
そして失敗の原因を探ったら、それを私たちはどのようにしていくべきかを考えてみます。次回で失敗しないためのコツを紹介する予定ですが、その導入部となるモデリングで失敗しない考え方を今回は紹介します。
モデルの失敗例
ここではモデリングを行った成果であるモデル図が、一生懸命がんばって描いたにも関わらず、結果的に失敗した例を見ていきます。この中にはモデリングの過程は問題なく実施したにも関わらず失敗したものもあります。逆にいい加減なモデリングのやり方をしても、成功したモデル図もあるかも知れません。まずはモデリングの過程は置いておいて、結果のモデル図だけを見て、失敗例を眺めていきましょう。
失敗例はいわば、モデルのアンチパターンです。反面教師として学ぶべき例です。同情も憐れみもいりません。ただマネをしないように、そうならないようにするだけです。
蜘蛛の巣のモデル図
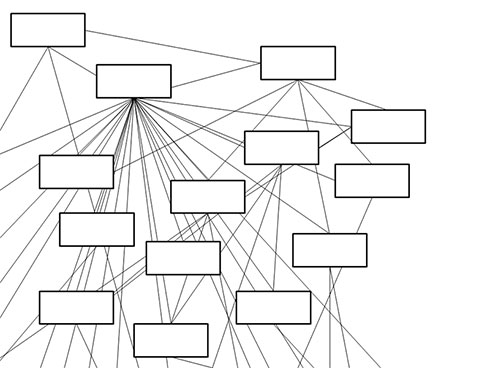
これはもう「蜘蛛の巣」と聞いただけで、このモデル図がどのように失敗したかが分かります。解説も言い訳も全く何もいらないものですが、それでもモデリングの最初の失敗例として見ていきましょう。図1に蜘蛛の巣状のクラス図を示します。
図1はまだかわいいと思う人もいるかも知れません。もっと真っ黒になっているクラス図を見たことがある人もいるかと思います。このクラス図は複雑怪奇、魑魅魍魎の図です。このクラスから、悪魔が出てきても怪異が出てきてもきっと誰も驚きません。逆にバグ除けのお札に使えそうです。
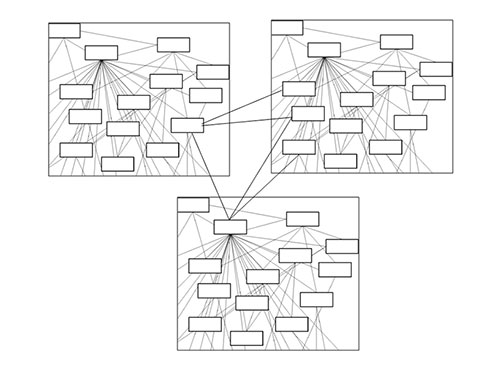
この蜘蛛の巣の取り除き方ですが、クラス関係をそのままにするときは、これは第3回でも紹介しましたが、グルーピングして階層化することになります。蜘蛛の巣から疎結合になっている蜘蛛の巣(サブグラフ)を見つけて、グルーピングします。図2に蜘蛛の巣をグルーピングする様子があります。
しかし図2のように疎結合になっているところがあればいいのですが、蜘蛛の巣のようになっている段階で疎結合な部分もないかも知れません。そこで次の手になります。
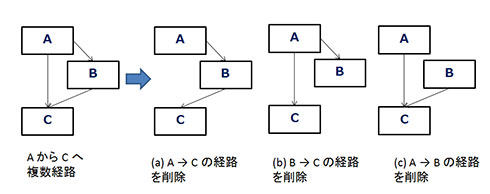
蜘蛛の巣になった図をキレイスッキリとするには、数を減らすしかありません。クラス図であれば、クラスとその関係をそのままにすることはもうできません。思い切って捨ててしまいます。そうなのです。こんがらがった蜘蛛の巣を解きほぐすには、1個1個捨てていくしかありません。このような地道なリファクタリングしかありません。(1)複数のクラスを1個にする、(2)複数経路の関係を減らすなどの方法でクラスやクラス間の関係を清算します。図3で複数経路の削除について紹介します。
図3のようにAからCへ複数経路があるとき、3個の関係の内、どれかを削除します。どれかを削除すれば、複数経路がなくなり、関係がすっきりします。このように三角関係はクラス図でも清算した方がいいでしょう。
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- 低価格FPGAでも文字認識AIの学習は可能なのか
- インフィニオンのSiC-MOSFETは第2世代へ、質も量も圧倒
- スバルが次世代「EyeSight」に採用、AMDの第2世代「Versal AI Edge」
- パナソニックの電動アシスト自転車にエッジAI機能を提供
- 自社開発のRISC-V CPUコアを搭載した32ビット汎用マイコン
- 東武ストアが指静脈による手ぶら決済を開始、酒類対応でセルフレジ利用率60%も
- CAN通信におけるデータ送信の仕組みとは?
- 過酷な資源ごみのビン色選別を自動化、PFUがイメージスキャナー技術から新規事業
- 組み込みシステム向けRTOSのシェアはTRON系が約60%
- CANプロトコルを理解するための基礎知識