標準偏差って何? 公差設計で生産バラツキを統計学的に考える:3D設計推進者の眼(30)(1/3 ページ)
機械メーカーで3D CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。今回は、生産のバラツキを統計学的に考えながら、標準偏差について解説する。
今回は、第27回「公差を緩くすればコストダウンできるわけではない」の続きの話をしましょう。第27回では「“バラツキ”を統計学的に考えてみましょう」というお話をしましたが、そこで出てきたのが、「正規分布」と「一様分布」でした。私の解釈では、量産型と個別受注生産型において、この分布の仕方を下図のように考えます。
私が経験してきたものは、「一様分布型−個別受注生産型」です。繰り返しになりますが、部品は装置の受注のたび、その必要な台数分だけ製作する必要があります。部品加工者は同じ部品でもそのたび、寸法公差・幾何公差が中央値に入るように部品加工をします。一度に大量に加工しないので、加工後の寸法中心値はその受注時の加工によって異なる可能性があります。
このことから、個別受注生産型の部品加工では、「正規分布」を取りながら、“ある区分”すなわち“許容値の中”を移動しているという「一様分布」という考え方が成り立つと考えました。
このように一様分布の分布を取る部品の組み合わせによって組み立てられた完成品の“管理したい寸法”はどうなるのでしょうか。
例えば、上図のように4個の部品により構成されている組立完成品があります。この組立完成部品は各部品1〜4の寸法により、5の寸法が管理できていると仮定します。この組立完成品は大量生産されず、そのため構成される各部品も大量生産ではなく、組立完成品の注文があるごとに部品加工されるものとします。
この時、1〜4の部品の管理寸法値は寸法公差内に納まりますが、加工の結果、その中央値は加工ごとに寸法公差内で移動しています。「中心極限定理」では、一様分布を持つ1〜4により求められる5の寸法は、正規分布上に存在すると“統計学的”に考えることができます。
これはサンプル数が多ければ多いほど、その傾向にあります。このことから、個別受注生産型では、
「その都度一発勝負だから」
「量産設計をするわけではないので」
「公差を厳しくすればいいから」
「管理したい寸法箇所は調整してしまえばいいから」
ということがいわれます。
一方で、個別受注生産型企業に装置を発注し、受け入れたお客さまからは、
「おたくの機械は機差(※1)が大きい」
「おたくにとっては受注生産品でも、うちは同じものを買っているのだけどね」
という声も聞いたこともあります。
このようなことからも、大量生産型の企業が考える、生産性やコストを重要視した上で、統計学的に公差計算・公差解析を行うこと良いのではないかと私は考えます。ちなみに、公差計算の例(1)の公差計算結果は下図のようになります。
今の設定公差値では、完成品の目標値±0.1mmに対しては、それ以上の範囲になります。確率的に±0.1mmを外れるのはどうかという視点でこの結果を検討する必要があるわけです。ここでは1〜4の初期の公差値の設定値での不良率になりますが、下図は√計算(不完全互換性の法則)で計算した結果になります。
100個の完成品を組み立てると、±0.1mmを満足できないものが6.68個発生することが、統計学的に考えられます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 知らないと取り返しがつかなくなる金型の費用と作製期間の話
- 3σと不良品発生の確率を予測する「標準正規分布表」
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- 幾何公差の基準「データム」を理解しよう
- Excelを使って周波数分析をやってみよう!
- 3D機構検証ソフトの最新版、干渉検証漏れ防止機能を搭載
- AI活用機能を強化した「AutoCAD 2025」「AutoCAD Plus 2025」をリリース
- 「データム記号」の使い方と設計者が身に付けておくべき作法
- FreeCADってどんな3D CAD? 簡単なモデリングから始めてみよう
- 位置度を考える上で重要な「最大実体公差」
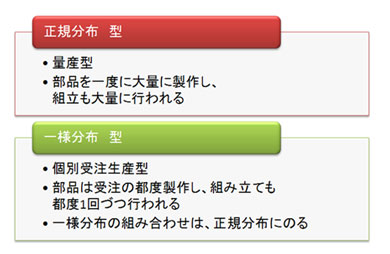 製造方式による正規分布と一様分布の分類
製造方式による正規分布と一様分布の分類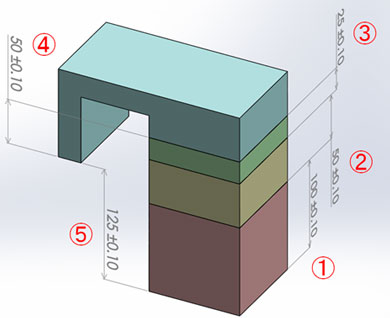 公差計算の例(1)
公差計算の例(1)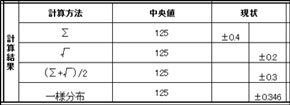 公差計算例(TOLJ:公差設計研究所 使用)
公差計算例(TOLJ:公差設計研究所 使用)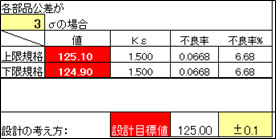 不良率の計算(TOLJ:公差設計研究所 使用)
不良率の計算(TOLJ:公差設計研究所 使用)

