バグ検出ドリル(6)いろんなところにバグがいる! 2分探索法の問題:山浦恒央の“くみこみ”な話(106)(2/4 ページ)
» 2018年05月14日 10時00分 公開
[山浦恒央 東海大学 大学院 組込み技術研究科 非常勤講師(工学博士),MONOist]
3.例題を基にした2分探索法のイメージ
無駄を省く手法の1つが、「2分探索法(binary search)」というアルゴリズムです。2分探索法は、検索するデータが中央値より高いか低いかを判断して探索します。なお、検索する配列の中身は、ソートしてあることが前提です。リスト1の配列を参考に、手順を示します。
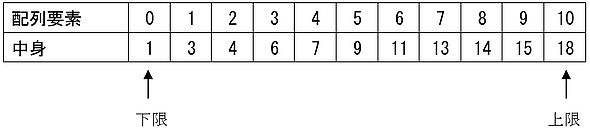
手順1:配列の探索範囲の下限(low)と上限(high)をセットします。例題では、左側が「0」で、右側が「10」ですね。
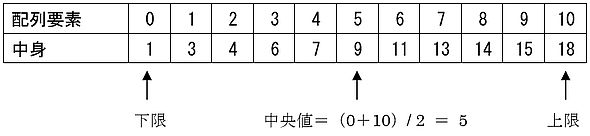
手順2:中央値(mid)の配列要素を算出し、下限≦上限が成立する間、繰り返します。つまり、中央値とは、下限と上限の配列要素を足し、2で割った値です。リスト1で、1回目は下限の配列要素が「0」、上限が「10」なので、中央値は(0+10)/2=5となります。
上記の計算を、「下限≦上限が成立する間まで繰り返す」、すなわち下限>上限となったら終了です。探索を続けていくと、下限と上限の関係が逆転するタイミングが現れます。
手順3:下記の3つのステップで、検索処理を実施する。
- ステップ1:中央の配列の中身が、検索したい数字と同じ場合、検索終了です。リスト1において、見つけたい数字が、「9」の場合は、1回目で終了となります。
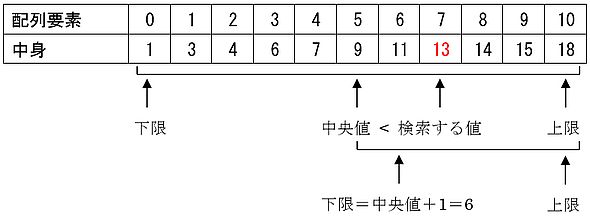
- ステップ2:「検索する数値>中央値の配列の中身」の場合は、中央値の配列要素より前に小さい数値が無いと分かります。よって、下限の配列要素=中央値の配列要素+1とし、手順2に戻ります。例えば、探したい数値が「13」、中央の中身が「9」の場合は、9より小さい値を見る必要がありませんから、「下限の配列要素=5+1」とし、手順2に戻ります。
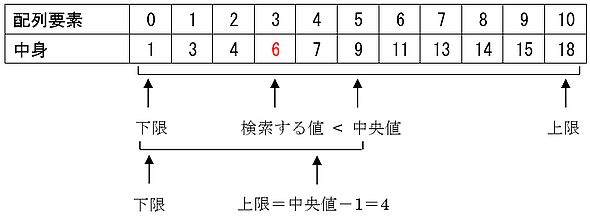
- ステップ3:「検索したい数値<中央値の配列の中身」の場合、中央値から先に、大きい数値が無いと分かります。よって、「上限の配列要素=中央の配列要素−1」とし、手順2に戻ります。例えば、探したい数値が「6」、中央の配列の中身が「9」の場合は、9より大きい値は見る必要がありませんから、「上限の配列要素=5−1」とし、手順2に戻ります。
目的とするデータにヒットしなかった場合、「上限の配列要素」や「下限の配列要素」を1つ加算、減算して、少しでも早く見つかるようにしているのかミソです。大体のアルゴリズムが分かったと思います。では、実際に問題に取り組みましょう。
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- 5G通信の遅延時間1ms以下は複数端末の制御でも可能か、東芝が量子技術で道を開く
- CAN通信におけるデータ送信の仕組みとは?
- イチから全部作ってみよう(7)正しい要求仕様書の第一歩となるヒアリングの手順
- CANプロトコルを理解するための基礎知識
- 組み込みシステム向けRTOSのシェアはTRON系が約60%
- インフィニオンのSiC-MOSFETは第2世代へ、質も量も圧倒
- 【問題7】10進数を2進数に変換するプログラム
- 景気減速でソフト開発の脆弱性対応が後手に? SBOM整備の取り組みも足踏みか
- テスト消化曲線とバグ発生曲線の7パターン診断
- 6Gに向けたサブテラヘルツ帯対応無線デバイス、100Gbpsの超高速伝送を実証
 リスト1 例題の配列
リスト1 例題の配列