組み込み技術者向けTLS1.3基礎解説(後編):IoTでTLS1.3を活用すべき3つの理由:IoTセキュリティ基礎解説(1/3 ページ)
インターネット接続機器のセキュリティ技術として広く用いられているTLSの最新バージョン「TLS1.3」は、IoTデバイスを強く意識して標準化が進められた。本稿では、組み込み技術者向けにTLS1.3の基礎を解説する。後編では、TLS1.3の具体的な変更点について確認し、IoT時代における活用の可能性を考えてみる。
1.はじめに
本解説記事の前編では、SSL/TLSに使われている基本的な暗号技術と典型的なメッセージシーケンスの概要を解説した。また、積み残されたTLSの課題を解決し新しい需要に応えることを目指してTLS1.3が策定されたことも紹介した。今回の後編では、TLS1.3の具体的な変更点について確認し、IoT(モノのインターネット)時代における活用の可能性を考えてみる。
2.危殆化暗号を排除して新しい暗号へ移行
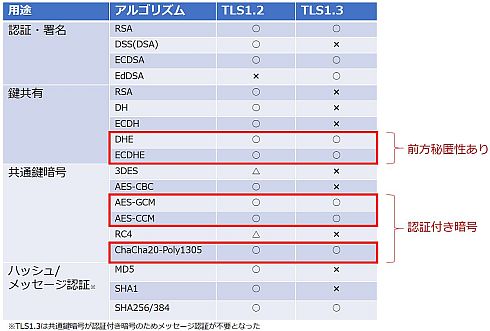
表1に示したのが、TLS1.2とTLS1.3、それぞれで利用可能な主要アルゴリズムの比較である。ここからは、TLS1.3においてなぜこのような変更が行われたのか、その理由について説明していこう。
暗号技術開発の歴史は常に解読技術とのいたちごっこであり、過去安全だった暗号を漫然と使い続けるだけでは通信の秘密を守り続けることはできない。技術動向を見極めながら、古くなった暗号は見直すなどの継続的な取り組みが必要だ。TLSにおいても、対応する暗号が危殆化したため利用禁止にする、脆弱性情報と対策を公開するなどして、随時、実装の更新が促されてきた。
共通鍵暗号のDES(3DES)やAESはブロック暗号とも呼ばれ、任意の長さの通信文を固定長ブロックに分割しブロック同士をつなげて暗号化する「Block Chaining」という演算を行う。その中で最もよく使われているのがAES-CBC(Cipher Block Chaining)だ。
ブロック暗号は最後のブロックを暗号化する際に「余り領域」が生じてしまうので、パディングというデータで空白を埋めて暗号化する。AES-CBCのパディングについては、実装に依存した脆弱性が指摘されており、パディングに関する実装の脆弱性を悪用して暗号文を解読する攻撃手法(パディングオラクル攻撃)も公開されている。こういった攻撃に対抗するには、個別のアプリケーションで意識的に正しい実装を行う必要があるが、対策が行き渡るまでには時間がかかる。古いソフトウェアは更新する予定すらないかもしれない。パディングの問題が指摘された当初は、AES-CBCの代替手段としてパディングが不要なストリーム暗号(ビットやバイト単位で逐次暗号化する方式)のRC4が推奨されたが、その後RC4も効果的な攻撃手法が発見されることになる。
これらの経緯を踏まえ、TLS1.3で使用する共通鍵暗号は攻撃リスクの小さい認証付き暗号(AEAD:Authenticated Encryption with Associated Data)を暗号スイートの標準とした。認証付き暗号とは、データの暗号化と同時にMACなどの認証用コードの演算を行うアルゴリズムのことだ。ブロック暗号では、AES-GCMやAES-CCMが認証付き暗号とされるが、性能が思うように出ないことが課題だった。特に、AES-NI(AESを高速処理する命令セット)を搭載したIntelプロセッサに比べ、組み込み分野で高いシェアを持つArmプロセッサはAESの性能が十分ではなかったこともあり、AES以外の選択肢も求められていた。
そこで、新しい認証付き暗号として期待されているのが、ストリーム暗号のChaCha20とメッセージ認証機能のPoly1305を融合したChaCha20-Poly1305だ。ChaCha20はシンプルなアルゴリズムであり、利用者側もシンプルに実装できるため実装依存の脆弱性が少ないとされている。加算剰余やビット演算のみで高速かつ安全な暗号化が可能で、実際にArmプロセッサによるソフトウェア処理ではAES-GCMと比較して性能が大きく改善したという報告もある。
TLS1.3では、EdDSA(Edwards-curve Digtal Signature Algorithm)という署名方式も追加された。署名は楕円曲線暗号を使ったECDSAが普及しつつあり、NIST(米国国立標準技術研究所)の規定するNIST P-256(secp256r1)という楕円曲線を使用するのが一般的だ。
ところが2013年に、NISTの規定した乱数生成アルゴリズム(Dual_EC_DRBG)に、米国のNSA(国家安全保障局)による解読用バックドアが仕込まれていたとの疑惑が浮上したために、NIST規定の楕円曲線の信頼性にも疑いの目が向けられるようになった。それ以後、EdDSAが「乱数を使わない」「NIST由来ではない」ことから注目され、代替の署名としての役割を期待されているようだ。EdDSAではCurve25519という楕円曲線を利用できるが、その処理速度の速さや安全性の高さにも関心が集まっている。
※)なお、これまで採用されてきたアルゴリズムのうち、3DES、AES-CBC、DSA、RC4、MD5、SHA-1、SHA224などは危殆化により削除された。
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- 5G通信の遅延時間1ms以下は複数端末の制御でも可能か、東芝が量子技術で道を開く
- CAN通信におけるデータ送信の仕組みとは?
- イチから全部作ってみよう(7)正しい要求仕様書の第一歩となるヒアリングの手順
- CANプロトコルを理解するための基礎知識
- ソニーのLPWA「ELTRES」の通信モジュールが機能追加、システムの簡素化が可能に
- 組み込みシステム向けRTOSのシェアはTRON系が約60%
- 【問題7】10進数を2進数に変換するプログラム
- インフィニオンのSiC-MOSFETは第2世代へ、質も量も圧倒
- テスト消化曲線とバグ発生曲線の7パターン診断
- 6Gに向けたサブテラヘルツ帯対応無線デバイス、100Gbpsの超高速伝送を実証