独立の原則を頭に入れて測定したり、アセンブリーを設計したりする:3D設計推進者の眼(35)(1/5 ページ)
機械メーカーで3D CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。今回は具体的にデータムとは何により決められているのかを説明する。
今回は「公差計算・公差解析」のお話について、「他国に負けない日本の設計技術の1つ」として話を続けましょう。前回は、「独立の原則」のお話をしました。
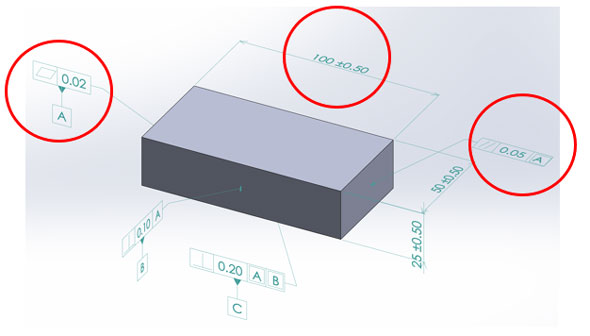
まず下図のようなモデルを例にて、「独立の原則」のおさらいをします。
このモデルの寸法(サイズ)公差と幾何公差の解説を行います。直方体モデルの左側面がデータムAです。このデータムAは0.02以内の平面によって構成されています。
直方体モデルの長手方向長さは100[mm]でその寸法(サイズ)公差は±0.5[mm]です。また右側面は、データムAに対し、平行度0.05以内になければならないと規定されています。
寸法は、99.5[mm]から100.5[mm]の間でバラツキがあることと、平行度は0.05以内にあるということは、別々に設定されています。一瞬「ん?」となるかもしれませんが、
「寸法(サイズ)公差と平行度公差領域が別々に設定されている」ということを言い換えると、「寸法(サイズ)公差と幾何公差が互いに独立して適用される」という「独立の原則」が成り立っているということになります。
幾何公差の測定方法
そこで幾何公差の測定方法を考える必要があります。平行度測定を考えてみます。最も簡単な方法とするのであれば、定盤基準に対するダイヤルゲージによる測定です。この場合は、測定物は定盤上に置かれるので、測定物のデータム面と定盤の基準面は同じになります。
別の方法としては、(接触式)3次元測定器による測定があります。この場合は、データム面と平行度を測定する面が見える状態で、3次元測定器のテーブルに置いて測定する場合もあります。
この測定での測定面は、その面上の複数点の測定データを最小二乗法などを用いた演算処理した測定面(理論的な仮想データム)を採用します。このため、ダイヤルゲージの測定とは異なる測定データによる算出となっていますので、注意が必要となります。
設計を行う上では、設定する幾何公差の機能を重要視しますが、加工方法を考えることと同じように、どのような測定方法を行うのか考えることも需要でしょう。
「測定方法も考えずに、安易に部品全数検査」などとISOのQC工程表に書いていないですよね?」
Vブロックを用いた真直度の測定、ここでお話しした平行度、輪郭度など、その幾何公差の測定方法に興味を抱かずにはいられません。
過去記事の「幾何公差と寸法公差、測定方法は何が違うの?」に詳細があるので、ぜひ参考にしてください。
ここまで説明したモデルの平行度の例で言えることは、平行度の値(例では0.05)は、寸法(サイズ)公差の値(例では0.5)に対して、小さな値を設定しています。もし、ここに平行度が設定しなかった場合は、データム面Aの対面は、99.5[mm]から100.5[mm]内にあれば問題ありません。
極端な例では加工面のうねりがありまながらも、下図のような状態でも許されますが、平面度が設定されていることにより、その公差域をさらに限られたものになっているわけです。
寸法(サイズ)公差だけの設定の場合に形状幾何公差が、寸法(サイズ)公差の公差域の中での幾何公差の公差を設定していることから、公差領域が更に制約され、加工のうねりはあるものの、データム面に対する平行である幾何特性を作っていることが、理解できることでしょう。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 知らないと取り返しがつかなくなる金型の費用と作製期間の話
- 3σと不良品発生の確率を予測する「標準正規分布表」
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- 幾何公差の基準「データム」を理解しよう
- Excelを使って周波数分析をやってみよう!
- 3D機構検証ソフトの最新版、干渉検証漏れ防止機能を搭載
- 「データム記号」の使い方と設計者が身に付けておくべき作法
- AI活用機能を強化した「AutoCAD 2025」「AutoCAD Plus 2025」をリリース
- FreeCADってどんな3D CAD? 簡単なモデリングから始めてみよう
- 位置度を考える上で重要な「最大実体公差」

 「独立の原則」説明モデル
「独立の原則」説明モデル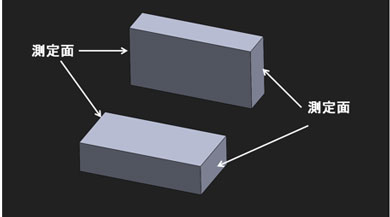 3次元測定器イメージ
3次元測定器イメージ



