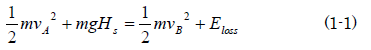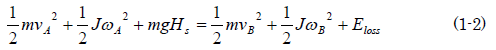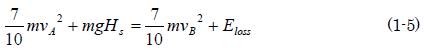摩擦があると、どうしてエネルギーを失うのか:ピタゴラスイッチの計算書を作ろう(1)(2/3 ページ)
線スロープの設計
まず、最初のサブ・システム1である曲線スロープを設計します。ボールが転がり始める、スロープの最初の位置Aの高さH が床から350mmで、スロープの底の高さHbが170mm、それから奥行きLが350mmという寸法制約があります。
銀二「ボールがスロープを登り切ったところの位置Bの高さは指定されていない。それに、ボールの材質や大きさの指定もないな」
草太「でも、『直線スロープ1に入るとき(B地点を通過)のボールの速さは極力小さいこと』って条件が付いているけど」
銀二「アトラクションとしては、早いスピードで深い谷を下って、上れるか上れないかギリギリの速度で上がってくる方がスリルがあるから、スロープの段差Hsもできるだけ小さい方がいいだろうな。段差Hsが大きいと2番目のサブ・システムに突入するときの速度は早くなるわ、シーソーに落下するときのボールの高さが低くなるわで、ほかのサブ・システムの設計が難しくなるからね」
草太「それぞれのサブ・システムが独立完結するような設計が、良い設計なんだね。2番目のサブ・システムに突入するときのボールの速度がほぼ0であるようになっていればいうことないな」
銀二「確かに直線スロープ1に突入するときの速度が0であれば、スリル満点だけど、下手すると速度が足りなくなって曲線スロープを逆走することが起きるかもしれないよ。だから、スロープを登り切ったときの速度が0となることを目標とする設計は、良い設計とはいえないな」
“スロープを確実に登り切ること”がまず重要で、次にB地点での速度ができる限り遅くなるように、どのパラメータをどのような値にしたらよいかを考えて、その根拠を示しながら行うのが良い設計だといえます。
草太「そのために段差Hsをいくらに設定したらいいか。それがサブ・システム1の最大のポイントだね?」
銀二「それだけでは不十分だ。必要な段差Hsの大きさは、スロープを転がるボールの材質にも関係してくるんだ。だからボールの選定も重要なポイントなんだ」
草太「ボールは何でもいいじゃない」
銀二「そんなことはないぞ。 重要なポイントだ。その理由を説明する前に、そもそも、段差Hsはなぜ必要だと思うんだい?」
草太「それは、ボールが曲線スロープを下るときにエネルギーを失うからさ。ボールがエネルギーを失うと勢いがなくなるから、その分低くしてやらないとスロープを登り切ることができなくなるでしょう。エネルギー損失がなければ段差Hsは0でもいいはずだけどね」
銀二「いまいったことを具体的に数式で説明してごらんよ」
読者の皆さんも草太と一緒に考えてみてください。
編集部より、読者の皆さまへ
以降で出てくる数式をメモ帳やノートなどに書き取るなどして、実際に計算しながら読み進めてみてください。より理解が深まります。
力学的エネルギーの保存と摩擦損失
草太「曲線スロープの終点Bを位置エネルギーの基準に取ると、スロープ始点Aと終点Bとの力学的エネルギーの関係はこうなると思うけど」
- mはボールの質量
- VA、VBは、それぞれ図1.1のA、B地点でのボールの速度
- gは(いうまでもなく……)重力加速度
- 左辺は「A地点での力学的エネルギー」
- 第1項は「運動エネルギー」
- 第2項は位置エネルギー」
- 右辺の第1項は「B地点での運動エネルギー」
- Elossはその損失する力学的エネルギー
草太「位置エネルギーの基準をB地点に取っているからB地点での位置エネルギーは0だから書いていないよ。ただし、A地点からB地点に移動するまでに力学的エネルギーが損失されるはずだね」
草太「つまり(1-1)の式は、『A地点でボールが持っていた力学的エネルギーは、B地点での力学的エネルギーと途中で失ったエネルギーの和である』ことをいっているんだ」
銀二「惜しいな。ちょっと足りないよ。ボールは回転しているだろう? だから回転の運動エネルギーが加わるんだ」
草太「なるほどね。で、どうなるの?」
銀二「草太、それで大学卒業できるのかい……。こうじゃないのか」
J はボールの慣性モーメント、ωA、ωBはそれぞれA、B地点でのボールの回転角速度です。ただしボールの回転は紙面と垂直な軸周りに回転し、この軸の方向は一定とします。
3次元で考えた場合、実際のボールの回転軸は揺れるのでしょうが、ここでは2次元として考えます。
銀二「こうでないと話が非常に難しくなるし、スロープにガイド機能を持たせればボールは2次元運動として扱えるだろう」
ボールの半径をrとする移動速度vと回転の角速度ωの関係
- 半径rの球体の慣性モーメントの計算公式
銀二「(1-3)と(1-4)を使うと、(1-2)の式は、こうなる」
銀二「(1-4)式は設計便覧を見ても載っているよ」
草太「おお、そうだった」
銀二「なーにが、『おお、そうだった』だよ。……それで、エネルギー損失がなければ、なぜHsは0でいいんだね?」
草太「あれれ?」
銀二「まず、スタート地点でのボールの速度は、ほぼ0に等しいだろ? だから(1-5)式の左辺の第1項は0だ。AからBへ移動するときのボールのエネルギー損失Elossを0とすれば、(1-6)のような式になる」
銀二「だから、スロープ終点Bでの速度が0でいいならHsは0とすることができるってわけだ。ところが実際にはエネルギー損失Elossは0ではないから……」
の段差が必要
草太「つまり曲線スロープを設計するためには、ボールがスロープを通過するときの力学的エネルギー損失Elossを計算する必要があるんだね」
銀二「そういうことだけど、その計算をする前に、力学的エネルギー損失はどうして発生するか分かっているかい?」
草太「摩擦が原因じゃないの?」
銀二「摩擦があるとなぜ、エネルギーを失うんだい?」
草太「だって、授業でそう教わったもの。力学的エネルギーがなくならなければ永久に運動し続けるけど、実際、運動は必ず止まるでしょ? それは摩擦によってエネルギーが損失するから、というのは常識じゃないの?」
銀二「うーん。その説明では、私の質問の答えになっていない」
Copyright © ITmedia, Inc. All Rights Reserved.