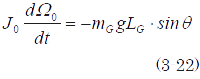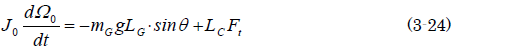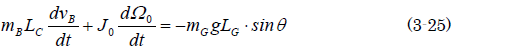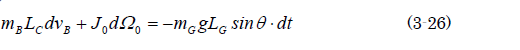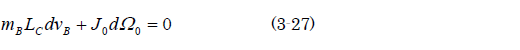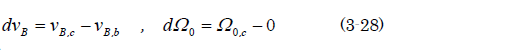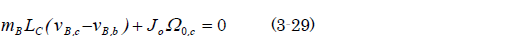ボールの運動軌跡が簡単に計算できるの?:ピタゴラスイッチの計算書を作ろう(3)(2/4 ページ)
ゲートの設計
銀二「つまりゲートには、
494から972mm/s
の速度範囲でボールが衝突するってわけだ。ゲートに必要な機能は、このボールをサブ・システム3へスムーズに渡すことだけど、どんな条件が必要だと思う?」
草太「まず、ゲートが重過ぎて、ボールがゲートと衝突した後止まってしまうのは困るね。次に、ゲートが軽過ぎてサブ・システム3のロック機構の止め板を飛び越してしまうのも困るな(図3.4)」
銀二「取りあえず、ボールがゲートで止まらない条件を求めてみようか」
草太「そうだね。ボールがさっきの速度でゲートに突入してきたときゲートを押しのけることができればいいんだね」
銀二「図3.5のようなボールの軌跡が得られればいいんだな。じゃあ、ボールの軌跡を求めてみよう」
草太「えっ? ボールの軌跡が計算で簡単に求められるの?」
銀二「お前はなんのために機械力学を学んだんだよ〜!」
銀二叔父さんはあきれてしまいました。しかし、かわいい甥っ子が困っているのだから、「まあ根気よく説明するしかあるまい」と腹をくくりました。
ボールとゲートが衝突したときの運動軌跡を求めよう
草太「単位を取るためだよ! ……というのは冗談として」
銀二「ほんまに冗談? まあ、そうだな。いきなり運動の軌跡を求めよっていっても抵抗あるか。じゃあ、ボールがゲートに衝突したときにゲートが開く最大角度を求めてみようか。いままで出てきた知識を使って、ゲートの最大開度を計算してごらん」
草太「エネルギーの保存式を利用するんだね。図3.6で、ゲートがボールと衝突した後のエネルギー保存の式は、ゲートの質量mG、慣性モーメントJGとして、ゲートの重心並進速度、回転角速度をそれぞれvG、ΩGとし、さらに衝突直後の状態を意味する添字をcとすると、ゲートが開いて重心の高さがHとなったときには、このようになるよね(図3.6)」]
草太「ゲートが最大に開いたときは、ゲートの運動は停止して、回転角速度
ΩGと並進速度vGは0となり、ゲート高さHは最大となるからエネルギーの保存式は、これ」
草太「エネルギー損失Elossは回転軸での摩擦損失だけだから小さく、ほぼ0だとして、さらに最大開度θmaxと最大重心位置Hmaxの関係を求めてみる」
だから、
となって、
上の(3-14)に注意して、
草太「しかし、衝突直後のゲートの角速度ΩG,cが分からん!」
銀二「JGってゲートの重心周りの慣性モーメントだね? (3-10)はゲートの重心の並進運動と回転運動のエネルギーを考えているけど、ゲートが回転する軸を回転中心とした物体の運動と考えれば、振り子の運動だね。この場合は回転運動だけを考えればよいから、回転軸周りの慣性モーメントをJoとし、回転軸周りの角速度をΩoと書くと、(3-10)から(3-15)、以下のようにも書ける」
ポイント:図3.6の、ゲートが張り付いた一点鎖線で描いた円が、回転軸を中心に回転すると考えると分かりやすい。
銀二「衝突直後のゲートの回転角速度は、重心周りも、回転軸周りも同じ値だからΩ0,c=ΩG,cだね。従って、(3-14)と(3-18)とを比較すれば、こうなることが分かる」
草太「これって、どこかで見た気がするな」
銀二「『慣性モーメントの平行軸の定理』ってやつだよ」
草太「おっ、そうだ、そうだ。……いや、それでも衝突直後のゲートの角速度Ω0,c=ΩG,cが分からんっていうことには変わりはない!」
運動量の保存
銀二「こういう場合は原点に立ち返って考えてみよう。まず、ボールとゲートの運動方程式を立ててみようか。ボールの運動方程式はボールの質量をmB、スロープ1を移動する並進速度をvB、衝突時にゲートから受ける力を
Ftとしたら、こうなる」
銀二「では、ゲートの運動方程式はどうなる?」
草太「ゲートは、振り子の運動と一緒だから、振り子の運動は、振り子の運動はー……確か授業で習ったはずだな……ノート、ノート……えっと、なになに」
草太「だそうです」
銀二「ノートを見ないと書けないのか。……まあいいよ。それで、その後どうする?」
草太「Ftはボールがゲートから受ける力だけど、作用反作用の法則により、ボールがゲートに作用する力でもあるから……」
銀二「本当はボールの回転ωについての運動方程式も考えるべきだけど、あまりにも複雑になるし、ゲートの運動にはあまり関係なさそうだから今回は省略しようか。しかし、(3-23)はモーメントの式だから単位はmNだろ。Fは力で単位はN(ニュートン)だよ。おかしくないかい?」
草太「そうか、回転軸から衝突点までの距離をLcとすると、こう」
草太「そして、この訳の分からんFtを(3-21)と(3-24)から消去してしまえば、こうなるよね」
草太「どうだ! 参った? ハッハッハ」
銀二「アホ。それで、どうやって衝突直後のゲートの角速度Ω0,cを求めるんだね」
草太「すんまへん。こっから分かりまへん」
銀二「まず、Ftというのは、どういう力だね?」
草太「ボールとゲートが衝突して互いに及ぼし合う力だよ」
銀二「じゃあ、ボールとゲートが接触していないときは0なんだな? ボールとゲートが金属のように硬ければ、衝突は一瞬だ。だから接触時間dtはほぼ0と考えていい。剛体の衝突の場合には(3-25)式の両辺に衝突時間dtを掛けると、こうなる」
銀二「だから、右辺はほぼ0に等しい。従って、以下のようになる」
銀二「これはいわゆる運動量保存の式だね。公式なんて知らなくたって、式を変形していけば自然に出てくるものなんだね。衝突直前のボールの速度をvB,b、直後の速度をvB,cとしよう。ゲートの角速度は衝突直前は0で、衝突直後の角速度はΩ0,cだ。だから、衝突前後の速度変化は、それぞれこのようになる」
よって(3-26)は、
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 有限要素法入門 〜連立方程式の解法、変位の計算〜
- 3σと不良品発生の確率を予測する「標準正規分布表」
- SUBARUが深層学習によるAI構築ツールを導入、プレス領域の成形解析工数の削減へ
- ムダのない作業と楽しさをもたらす“ありそうでなかった発想”
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- パナソニックが再生家電を売る理由、サーキュラーエコノミーだけが目的ではない
- 幾何公差の基準「データム」を理解しよう
- 「設計者はなぜCAEを煙たがるのか」を考察し、広がりを阻害する壁を取り除く
- 「デザイン経営」とは? なぜデザインが経営に貢献できるのか
- ARで掃除した経路をリアルタイムで可視化、ダイソンが無駄のない掃除体験を提案
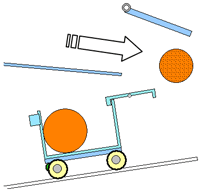 図3.4 ボールがロック機構を飛び越す
図3.4 ボールがロック機構を飛び越す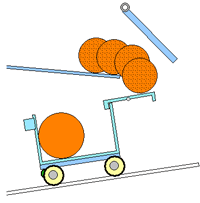 図3.5 理想的な軌跡
図3.5 理想的な軌跡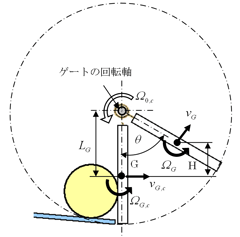 図3.6 衝突後のゲートの運動
図3.6 衝突後のゲートの運動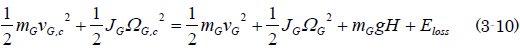
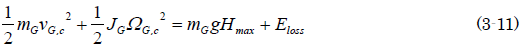

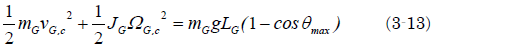

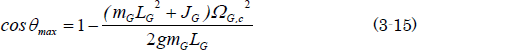
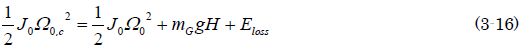

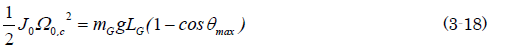


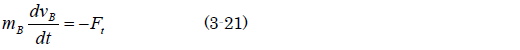
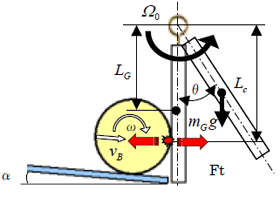 図3.7 衝突時の力と運動
図3.7 衝突時の力と運動