ボールの運動軌跡が簡単に計算できるの?:ピタゴラスイッチの計算書を作ろう(3)(3/4 ページ)
反発係数
草太「おぉ! やっとΩo,cが出てきた! しかし、衝突直前のボールの速度vB,bは分かっても、衝突直後の速度vB,cが分からへん!」
銀二「どーこーのだーれだーかしーらなーいけーれどー」
草太「なにそれ?」
銀二「月光仮面の主題歌。どこの誰だか知りませんが、反発係数ってやつを考えた人がいてね……。あ、ちなみに月光仮面は私がまだ小さいころに……」
草太「そうや、そうや。反発係数eを使えばいいんや。これは分かるもんね」
分母はゲート衝突面から見た衝突前のボールの衝突方向の速度で、分子はゲートから見た衝突後のボールの跳ね返り方向の速度です。反発係数eというのは、衝突面と垂直方向の速度変化に対して定義しています。
草太「マイナスが付いているのは衝突後には速度が反転するからだ。いずれにせよ、反発係数というのは、衝突前後の衝突物体間の相対速度比だね」
銀二「月光仮面、無視されてもうた(ショボン……)」
草太「(3-29)と(3-31)を整理して書きそろえるよ」
草太「Ωo,cとvB,cの2元連立方程式となり、そしてこの解は?」
草太「やったね! これで衝突直前のボールの速度vB,bから、衝突直後のボールの速度vB,cとゲートの角速度Ωo,cが計算できる! じゃあ、早速衝突直後の速度を求めてみようか」
条件
- ゲートの材質→ポリカーボネート製。質量は8.5g
- ヒートンの質量は1個0.9g
- ゲートとヒートン2個の合計は、mG 。つまり、mG=10.3 g
- 寸法は高さH=42mm、厚さt=4mm
草太「まず、幅方向を回転軸とした矩形物であるゲートの重心周りの慣性モーメントは、設計実用便覧に載っている公式だね」
JG=10.3×(422+42)/12=1.53×103(g−mm2)
草太「ただし、回転軸からのモーメントは平行軸の定理を使う」
≪J0=JG+mG・LG2=1.53×103+10.3×292=1.02×104(g−mm2)
草太「反発係数はe=0.83としてみよう。速度vB,bは494から972 mm/s。cos(5°)=0.996として、これらを(3-33)に代入する」
(3-35)のΩo,cを(3-19)に代入すれば 、
cos(θmax)=0.768〜0.102
だから……
θmax=39.8〜84.2 度
草太「図に描くと図3.10のようになるね」
銀二「84.2°はいいけど、39.8°は角度が小さくて不安だね。衝突後のボールの速度も遅くなっているし、跳ね返って戻ってきたゲートとボールが再衝突してボールが止まるってことはないかな?」
草太「いわれてみればそんな気もするね。じゃあ、どうするの」
銀二「そうなるか確認してみよう」
草太「どうやって?」
銀二「2つの方法がある。1つは、手計算による近似計算で確認する方法。もう1つはシミュレーションでの確認。シミュレーションをする前に近似計算してごらん」
草太「計算してみろといわれてもな……」
ゲートと衝突した後、ボールは直線スロープ1の端に来るまではスロープの上を直線的に移動しますね。走り出す速度は、衝突直後の速度で、重力加速度gによる力の傾斜分力が作用するので、g・sin(5°)の加速度が作用している場合と同じです。
草太「ふむふむ。だからボールが斜面に沿って動く距離をsとする」
*gは重力加速度で9810mm/s2。sinの( )内の単位はラジアン
草太「一方ゲートとの衝突点から直線スロープ1の端までの距離sを出す」
草太「だから、(3-35)のvB,c=17.9 mm/sの場合、(3-36)と(3-37)から、t=0.156secでは、ボールは端から落ち始めることが分かる。このときにゲートはどの位置にあるか?」
銀二叔父さんが助け舟を出そうかと思ったところ……。
草太「あ。ゲートの運動は振り子だといっていたよな。じゃあ、振り子の周期は?」
そうだそうだ。銀二叔父さんは心の中でうなずきました。ゲートが最大開度に達して元の位置に戻るまでには周期の半分の0.17secということになるわけです。
草太「衝突後0.156secのゲートの位置が分かればいいのにな」
草太「t=0.156secのときのゲートの角度はこうなるね」
草太「衝突後、ボールがスロープの端に来る時刻のゲートの位置を描いた図3.11を見れば、ボールが落下する前にゲートと再衝突することが分かる」
銀二「お見事! よく分かったじゃないか」
草太がゲートの材料に使おうとしていたポリカーボネート製のネームプレートでは、ボールがサブ・システム1の曲線スロープからサブ・システム2の直線スロープ1へギリギリの速度で移る場合には、ボールがゲートで止まってしまう可能性があるということが分かりました。
もちろん、曲線スロープから直線スロープへは、実際にはある程度の速度で入ってくるので、絶対にゲートでボールが止まるとは限りません。しかし、限界状態で考えた場合その危険があります。
銀二「そこで、別の材料でゲートを作るという選択も出てくるわけだ」
草太「ベニヤ板の切れ端があるから、それで作ろうかな。密度もポリカ(PC:ポリカーボネート)の半分程度だしね。でも、この計算をまたやるのは面倒だなぁ」
銀二「Excelを使えばいいじゃないか」
草太「あ、そうね」
ボールがゲートと衝突するときの速度vB,bをパラメータとして、ゲートの質量mGを変数とした場合の最大開度θmaxは(3-33)と(3-19)を使えば簡単に計算できます。ただし、戻ってきたゲートとボールとの再衝突によってボールがゲートを通過できなくなるかどうかまでは判断できません。
それに、これまでの計算はあくまで近似計算です。衝突時のボールの回転の影響は考慮に入れてないので、衝突後のボールの運動については若干精度を欠いているわけです。
銀二「じゃあ、シミュレーションでもやってみようか。もっともシミュレーションも近似計算だけど手計算よりは精度がはるかに高いからね」
銀二叔父さんは草太のパソコンにソフトをインストールして、シミュレーションを始めました。
その結果を図3.12と図3.13に示します。シミュレーションのアニメーションを動画3.1に示します
手計算とシミュレーションの傾向は非常によく似ています。ただし手計算の結果からは、衝突後ボールがゲートを通過せずゲートの前で停止してしまうかどうかは直接分かりません。グラフから推定するしかありません。しかしシミュレーションでは9g以上の質量を持つゲートではボールが通過せず停止してしまうことがアニメーションから簡単に分かります。
銀二「やっぱりネームプレートを使うのはやめておいた方がいいな」
草太「そうだね。板の切れ端で作ってみるよ」
実験検証
1週間後、銀二叔父さんは草太からこんなメールを受け取りました。
銀二叔父さんから2つの宿題
銀二叔父さんは、また以下のような宿題を2つ置いていきました。
問題1
前回の問題1のように曲線スロープでの転がり摩擦係数を0.05とした場合、ボールとゲートが衝突したときのゲートの最大開度θmax、衝突後のボールの速度の速度vB,c、衝突後、ボールが直線スロープ1の端に到達するまでの時間、その時間におけるゲートの開度を求めよ。
ただし、直線スロープ1でのボール運動エネルギーの損失は無視し、ボールとゲートの特性値はそれぞれ下記の値とする。
- ボールとゲート間の反発係数e=0.83
- ボールの質量mB=6.7g
- ゲートの質量mG=10.3g
- ゲートの回転軸回りの慣性モーメントJo=10200g・mm2
- 回転軸から衝突点までの距離Lc=36.9 mm
- 回転軸からゲート重心までの距離LG=29 mm
- 直線スロープ1傾斜角α=5°
問題2
動画3.2のボールの反発係数eを求めよ。
回答は、4ページ目にあります。
さて、次回はいよいよ、台車と台車のロック機構の設計です。ご期待を!(次回に続く)
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 知らないと取り返しがつかなくなる金型の費用と作製期間の話
- 3σと不良品発生の確率を予測する「標準正規分布表」
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- 幾何公差の基準「データム」を理解しよう
- Excelを使って周波数分析をやってみよう!
- 3D機構検証ソフトの最新版、干渉検証漏れ防止機能を搭載
- 「データム記号」の使い方と設計者が身に付けておくべき作法
- AI活用機能を強化した「AutoCAD 2025」「AutoCAD Plus 2025」をリリース
- FreeCADってどんな3D CAD? 簡単なモデリングから始めてみよう
- 位置度を考える上で重要な「最大実体公差」

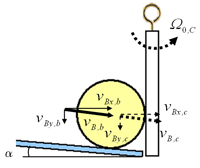 図3.8 衝突前後の速度
図3.8 衝突前後の速度
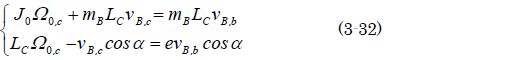
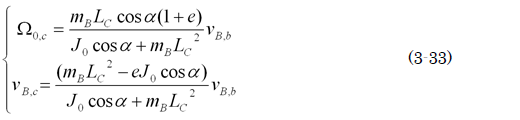

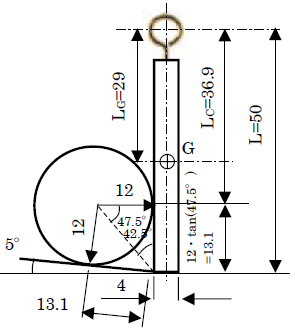 図3.9 ゲートの寸法
図3.9 ゲートの寸法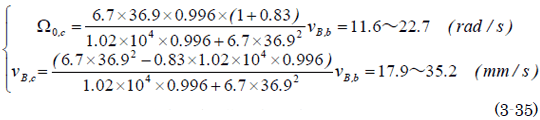
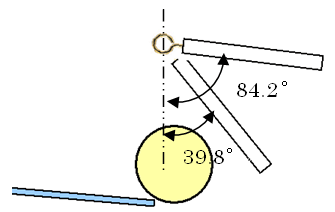 図3.10 ゲート最大開
図3.10 ゲート最大開

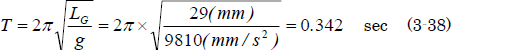
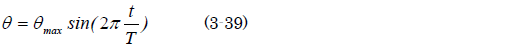
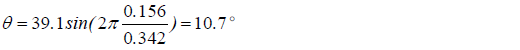
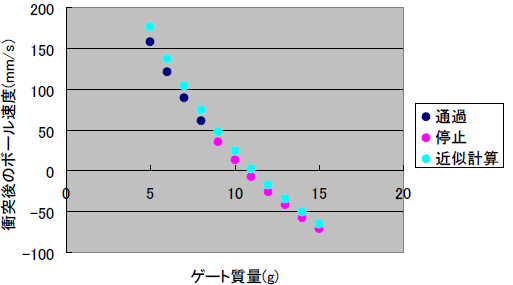 図3.11 衝突後、0.148sec後のゲート開度とボール位置の予測
図3.11 衝突後、0.148sec後のゲート開度とボール位置の予測 図3.12 ゲート質量と衝突後のボール速度との関係(シミュレーション
図3.12 ゲート質量と衝突後のボール速度との関係(シミュレーション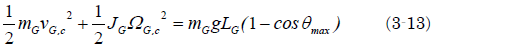 図3.13 ゲート質量とゲート最大開度との関係(シミュレーション)
図3.13 ゲート質量とゲート最大開度との関係(シミュレーション)