直交配列実験を基にした重回帰分析の実務:Excelで学ぶ実験計画法の基礎(4)(5/5 ページ)
データ2の解析
2番目のデータは、特性値に影響する要因として、2つの因子が取り上げられた実験のデータです。このように2つの因子を対象に実施する実験は二元配置実験と呼ばれ、対応する統計的仮説検定の方法は二元配置分散分析でした。二元配置分散分析には因子間の交互作用を検定する“繰り返しのある”場合の方法と、交互作用を検定しない“繰り返しのない”場合の方法があります。
方法の選択は、実験のやり方に依存し、2つの因子の水準の組み合わせについて、2回以上の測定を実施した場合が繰り返しのある方法、1回しか測定しなかった場合が繰り返しのない方法になります。2番目のデータは、繰り返しのない実験のデータです。2因子の繰り返しのない実験のデータは、そのままの状態でデータがグラフ化できます(図21)。
まず各因子の効果ですが、感光剤の種類で差があり、機械の種類にも差があることが分かります。次に交互作用です。グラフを見ると線が平行になっていて、交互作用のないことが分かります。グラフが平行でない場合、交互作用の存在が示唆されますが、繰り返しのない実験では、交互作用の統計的有意性が数学的な制約から検証できないので、再実験を行いデータを追加して、繰り返しのある場合の方法で検定を実施します。二元配置分散分析の結果は図22のとおりです。感光剤、機械ともに効果が有意であることが分かります。
データ3の解析
3番目のデータは直交配列実験のデータです。分散分析は残念ながらExcelでは直接実施できないので、今回ご紹介した因子の効果を重回帰分析にて分析した結果を示します(図23)。因子間の交互作用は考慮していません。補正R2は0.719で予測の精度は高いといえます。しかし、分散分析の有意Fは0.097で0.05を下回らないため有意ではなく、この結果を一般化できるとはいえません。実験のデータに限り因子の効果について考察を述べるのであれば、因子Bの係数の値がほかの因子より大きく特性値への影響度が高いといえます。
図23 重回帰分析用01データ
◇
以上、最終回まで、実験データの解析がメインになってしまいましたが、重要なのは実験の計画とデータ収集です。その話題は第1回の記事で復習していただくとして、皆さんには、本連載の記事を何らかの糧に、データに基づいた品質管理を実践していただければ幸いです。
関連記事
- 「Excelで学ぶ実験計画法の基礎」最新記事一覧
 本当の「タグチメソッド」を誤解していませんか?
本当の「タグチメソッド」を誤解していませんか?
コトバばかりが先行している感のあるタグチメソッド。あなたは本質を誤解していませんか? SN比や直交表だけではない本当のタグチメソッドを知ろう あなたが品質管理で果たすべき役割は何か
あなたが品質管理で果たすべき役割は何か
製造現場で実施する製品管理を中心とした品質管理の基本を解説する。組織における品質管理の在り方から先人の教訓まで、筆者の経験とノウハウを紹介。
Copyright © ITmedia, Inc. All Rights Reserved.
製造マネジメントの記事ランキング
- コニカミノルタと富士フイルムBIが複合機の調達業務で合弁協議、トナーの提携も
- 中小製造業の2人に1人が「毎日FAX使う」、DXが進まない要因とは
- オリンパスの新CMOが担う「MSA」の役割とは、内向きではなく患者と向き合う
- 「スキルデータ」の活用が製造業にもたらすメリットとは 実践事例と注意点を解説
- 製造業DXで日本が欧州から学ぶべき点、学ばなくてもよい点は何か
- 見積もり時間をゼロに 部品の納期と金額を即時算定するミスミの新システム
- 試行フェーズを脱した通信業界の生成AI活用 MWC 2024レポート(後編)
- パナソニックとリオンが「次世代補聴器」を共同開発へ アライアンス締結
- 品質管理に必須の統計的手法「X-R管理図」「P管理図」の作り方
- 新会社名は「ETRIA」 リコーと東芝テックの複合機開発/生産事業統合へ
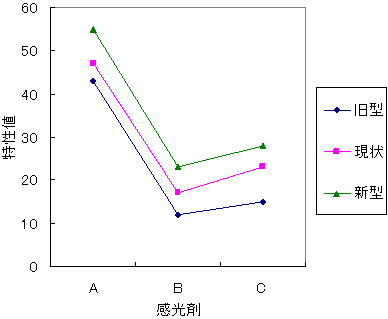 図21 繰り返しのない二元配置分散分析
図21 繰り返しのない二元配置分散分析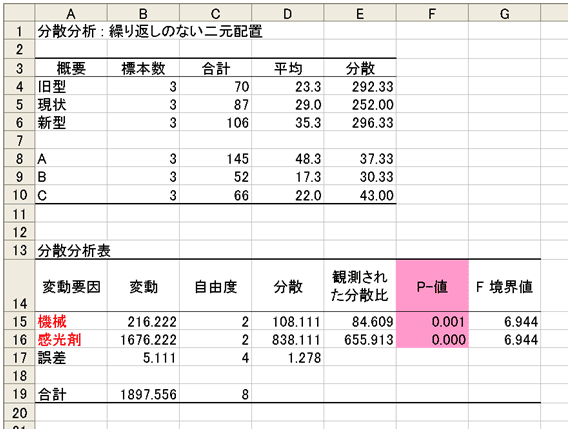 図22 データ2の二元配置分散分析の結果
図22 データ2の二元配置分散分析の結果



