ラプラス変換と割り切ったお付き合いをするよ:独学! 機械設計者のための自動制御入門(6)(2/4 ページ)
ついに出た! ラプラス変換
ついに出てきましたか……(ラブプラスならよかったのにね)
ラプラス変換は使いたくなかったけど、これを使わんと、かえって難しく、かつ面倒くさいことになるからな。ラプラス変換については、ここでは、取りあえず、道具として機械的に利用することにしようや
そうだね。難しいこといわれてもよく分からないし……
ここでは、『ラプラス変換』とは『物体の運動や物理状態を表現する微分方程式を代数方程式(掛け算とか割り算)に変換して表現したもの』と考えてほしい。ここから、先は、道具の使い方の説明だと思って、割り切って聞いてな
分かったよ
入力xをラプラス変換したものを『L(x)』と書くことにしよう
出力yは、『L(y)』だね
そうや。入力xに比例定数Aを掛けたものが出力yである場合、ラプラス変換したもので表現すると、
y=A・x ⇒ L(y)=A・L(x) (3)
で、何も変わらへん
普通の掛け算と同じだ
しかし、微分や積分はちょっと違う。出力yが入力xを微分したものである場合に、ラプラス変換したもので表示すると
『s』は『ラプラス演算子』だと習ったよ。でも、sが何を意味するのか、さっぱり理解できなかったよ
ここでは、sの数学的説明はせえへんでー。ラプラス変換という道具の使い方の説明に終始するわ
分かったよ。じゃあ、出力yが入力xを積分したものである場合は?
その場合はこうだ
取りあえず、これだけ覚えれば、道具としてのラプラス変換を使うことができる
微分はsを掛け、積分はsで割る。じゃあ、s2を掛けるのは、2回微分することで、s2で割ることは、2回積分することになるんだね
そういうことやねん
だからラプラス変換は、微分方程式を代数方程式に変換しているっていうんだね
それだけやないんや。ラプラス変換を使うと、ボード線図が簡単に描けるんや!
ラプラス変換を使って、バルブモータコントローラの新たな伝達関数G1のボード線図を描く前に、図1の浴槽の水位制御のブロック線図を、ラプラス変換表示してみましょう。
(1)の微分方程式をラプラス変換すると、
となります。代数演算によって整理すると、
となり、ラプラス変換した伝達関数G1は、
です。
上の計算は、ブロック線図でも表すことができます(図3)。
これに比例要素を並列に加えると、図4になります。
同様に、G3については以下のとおりです。
伝達関数のラプラス変換表示は、こちら。
大文字のSは浴槽の断面積です。ラプラス演算子の小文字sと紛らわしいので注意してください。そして、バルブ−流量特性G2は、以前と同じような式となります。
バルブモータコントローラの伝達関数G1について、ラプラス変換を使って比例+積分とした制御システムのブロック線図を表示すれば図5になります。
ラプラス変換を使えば、バルブモータコントローラの伝達関数G1を、まるで分数のように計算できることは分かったよ。で、どうやって、G1の周波数応答特性、つまりボード線図を描くことができるのさ?
実はな、草太が、なんのこっちゃ分からんかったラプラス演算子sを
s=i・ω (12)
と置いて、計算すればいいんや。なんで、そうなるかは、ここでは説明せえへんよ
その理由は自分で勉強して理解することにするよ。とにかく、周波数ω(rad/min)に虚数iを掛けたものをsとすればいいんだね。すると……
で、ここからどうする?
さっきいったやろ、代数として計算すればいいって
あ、そう。じゃあ……
ωを0から+∞まで変化させたときのG1の絶対値と位相を計算すればボード線図が求まるやん
では、実際にボード線図をどのように作成するか説明してみましょう。
まず伝達関数G1は、絶対値をA、位相をθとすると、オイラーの公式より、
と書けます。
ですから、
となります。(17)式からG1の絶対値A、位相θを計算することができます。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 知らないと取り返しがつかなくなる金型の費用と作製期間の話
- 3σと不良品発生の確率を予測する「標準正規分布表」
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- 幾何公差の基準「データム」を理解しよう
- Excelを使って周波数分析をやってみよう!
- 3D機構検証ソフトの最新版、干渉検証漏れ防止機能を搭載
- AI活用機能を強化した「AutoCAD 2025」「AutoCAD Plus 2025」をリリース
- 「データム記号」の使い方と設計者が身に付けておくべき作法
- FreeCADってどんな3D CAD? 簡単なモデリングから始めてみよう
- 位置度を考える上で重要な「最大実体公差」






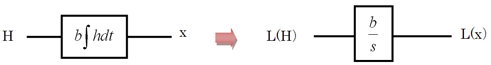 図3 ラプラス変換の計算をブロック線図で表す
図3 ラプラス変換の計算をブロック線図で表す 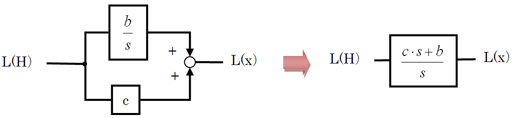 図4 比例要素を並列に加えてみた
図4 比例要素を並列に加えてみた 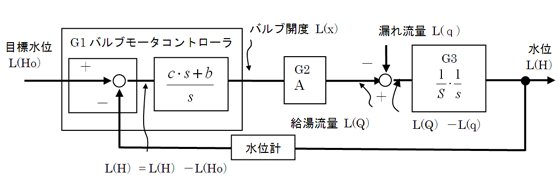 図5 比例+積分制御による浴槽水位制御ブロック線図
図5 比例+積分制御による浴槽水位制御ブロック線図 



