制御設計の基本! ボード線図を極めよ:独学! 機械設計者のための自動制御入門(9)(1/4 ページ)
制御設計の実務能力を養うために、ボード線図の作図操作やその見方によく慣れておこう
当連載の登場人物
銀二(ぎんじ)
設計コンサルタント。甥(おい)っ子の草太を自分の息子のようにかわいがっています。
草太(そうた)
銀二の甥。現在は大学院生です。ちょっと困るとすぐ叔父を頼ってしまうちゃっかり者だけど、頑張り屋さんです。
編集部注* 本記事はフィクションです。実在の人物団体などとは一切関係ありません。
前回は、フィードバックシステムの応答性は、開ループ伝達関数Goの周波数ゲイン特性によって決まることを説明しました。開ループ伝達関数Goのボード線図において、ゲイン曲線が0dBとなるカットオフ周波数が高ければ高いほど、その閉ループシステム(フィードバックシステム)は応答性のよいシステムであることが予想されます。従って、応答性を改善するためには、位相余裕を減少させずに開ループ伝達関数Goのゲイン曲線を上に上げればよいことになります。その補償方法は微分補償であることも説明しました。そして、比例、積分、微分の各補償要素を並列接続したものがPID制御(PID補償制御)でした。
このようにフィードバックシステムにおける補償設計は、開ループ伝達関数Goのボード線図のゲイン曲線と位相曲線を使っておこないます。従って、制御設計の実務能力を養うためには、ボード線図の作図操作や見方に慣れておく必要があります。そこで今回、第4回で学んだボード線図について復習し、ボード線図についての理解を確実なものにしましょう。
ボード線図の描き方の復習
ラプラス変換を使わないボード線図の描き方は、第4回で説明したな
確かに、教えてもらったね。『ボード線図上では、伝達関数の掛け算は足し算になる』っていってたね。伝達関数G1の振幅比をA1、位相遅れがθ1、伝達関数G2の振幅比A2、位相遅れθ2とすると、伝達関数G1・G2の振幅比はA1・A2、位相遅れはθ1+θ2となる。つまり……
ならば
このことを図1の正弦波の絵で説明してくれた
ボード線図のゲイン特性の縦軸は振幅比の対数だから、G1・G2のゲインは20・loG(|G1・G2|)=20・loG(|G1|)+20・loG(|G2|)となって、G1とG2のゲインの足し算になる。一方位相特性の縦軸は“生”の位相の値そのままだから、G1・G2の位相はそれぞれの位相の足し算になる
そうやったな。伝達関数が複素指数関数で表現できるってことを知っていると、そのことが、さらに、いっそうよく理解できる。つまり……
だから
『ボード線図上では、伝達関数の掛け算は足し算になる』というのは、結局、『指数関数の掛け算』のことをいってるんだよね
そういうこっちゃ。草太が『もっとボード線図に慣れたい』っちゅうから、前回説明した横風を受けるときの自動走行制御システムのブロック線図(図2)を、図3のように描いてみたんやけど、どや? 分かるか?
要素ブロックにそれぞれのボード線図を当てはめて描いたんだね。うん。図2より分かりやすい気がする
じゃあこれからは、図3のブロック線図をベースに、制御設計がどのようにして行われていくか考えてみようか。 まず、図3のブロック線図のコントローラG1がP(比例)制御要素のときについて考えてみよう。比例制御の伝達関数をGPと書くことにしよう。GPの比例係数をKPとして複素指数関数で表記すれば、比例制御の伝達関数GPは……
すると、ゲイン特性、位相特性はそれぞれどうなる?
(1)からゲインは
位相は……
じゃあ、コントローラG1をPI制御にしたらどうなる? P制御とI制御の比例係数はそれぞれKP、KIとして、その伝達関数をGPIとしようか
PI制御は図4に示すように、比例要素と積分要素を並列に加算したものだから、こうだよね
そうや。それで……
……確か、普通に計算すればよかったから……
……で、次どうする? そうだ……、s=i・ωと置いて……
ちょっと待ちぃ。s=i・ωと置く前に質問や。(3)はどういう構成の式やと思う?
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 有限要素法入門 〜連立方程式の解法、変位の計算〜
- 3σと不良品発生の確率を予測する「標準正規分布表」
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- SUBARUが深層学習によるAI構築ツールを導入、プレス領域の成形解析工数の削減へ
- ムダのない作業と楽しさをもたらす“ありそうでなかった発想”
- パナソニックが再生家電を売る理由、サーキュラーエコノミーだけが目的ではない
- 幾何公差の基準「データム」を理解しよう
- 「設計者はなぜCAEを煙たがるのか」を考察し、広がりを阻害する壁を取り除く
- 「デザイン経営」とは? なぜデザインが経営に貢献できるのか
- フローで考える流れのモデリング(その2) 〜適用例と3D/1Dの関係〜


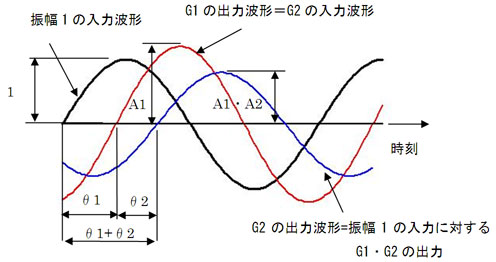 図1 伝達関数G1・G2の入出力波形
図1 伝達関数G1・G2の入出力波形 
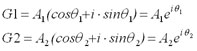
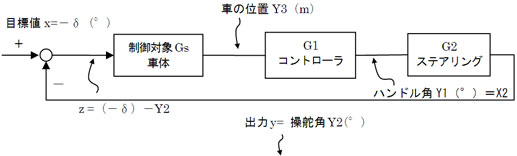 図2 横風を受けるときの自動走行制御システムの構成
図2 横風を受けるときの自動走行制御システムの構成 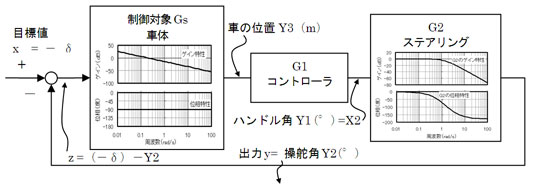 図3 横風を受けるときの自動走行制御システムの構成(銀二さんが図2を描き直した)
図3 横風を受けるときの自動走行制御システムの構成(銀二さんが図2を描き直した) 
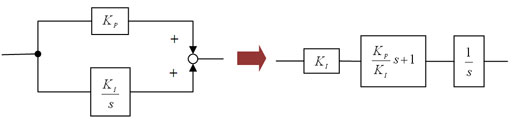 図4 PI制御のブロック線図
図4 PI制御のブロック線図 



