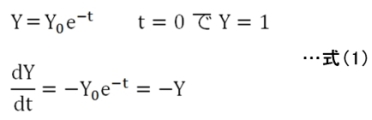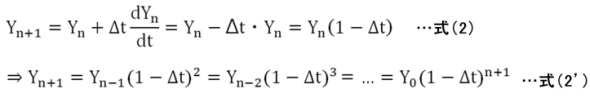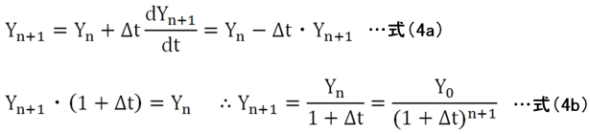SPICEの過渡解析（その1）：キャパシタンス素子の場合：SPICEの仕組みとその活用設計（4）（1/3 ページ）

　前回までは非線形を含む静解析について説明してきましたが、今回は回路解析で欠かせない過渡解析について紹介します。静解析に対して、動解析あるいは非定常解析と呼ばれるときもあります。

　過渡解析とは、いわゆる時間的に変化する特性を解析するものであり、回路解析で時間的に電圧・電流が変化する部品としてはキャパシタンス素子とインダクタンス素子があります。今回はその中のキャパシタンス素子を取り上げます。

次ステップの値を予測するには

　ご存じかもしれませんが、過渡現象問題を扱う場合に常に問題となるのが、「次ステップの値をどのような手法で予測するか」です。例えば、明日の天気を予測する場合を考えてみましょう。

（1）1つの方法としては、「夕焼けなら明日は晴れ」とか「朝焼けは雨」と言われるように、今時点や過去の天気情報を使って明日の天気を予測する手法です。予測に使う関数は型式も係数も決まっていて結果を計算するだけなので、この種の関数はExplicit（陽）関数と呼ばれ、この手法を陽解法と呼びます。

（2）もう1つの手法としては、さまざまな明日の天気を仮定し、その天気になるためには今の天気はどうあるべきかを考えます。例えば、「明日が晴れと仮定するなら今の湿度は減少しているはず」や、「明日が雨なら今の湿度は増加しているはず」などです。そして、その中から今の天気情報と合致するケースを明日の天気とする方法です。

　この手法では、予測する明日の天気を単純計算で決めることができず、さまざまな仮定された明日の天気の中から今の天気情報と合致する明日の天気を選び抜かねばなりません。関数の型式は決まっていても係数を決めるための方程式を解く作業が計算サイクルの都度に必要になるのです。

　この種の関数を前述の陽関数に対してImplicit（陰）関数と呼び、この手法を陰解法と呼びます。

　なお、予測に使う微分方程式を差分方程式で表現する場合、陽解法を前進法、陰解法を後退法とも言います。

前進法と後退法の特徴

図1　前進法と後退法のイメージ（クリックで拡大）

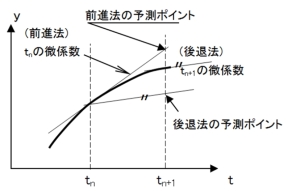
　差分方程式の1次近似を採用する場合をオイラー法と言います^＊1）。1次近似ですので、時間の刻み区間内（t_n〜t_n＋1）の変化を接線で近似することになります。接線の傾斜とは関数の微係数のことなので、次ステップの値を予測する直線の傾きには、

• 前進法（陽解法）では現時刻t_nの微係数
• 後退法（陰解法）では次時刻t_n＋1の微係数

を使うことになります（図1）。

＊1）今回採り上げたオイラー法は数学的にはテイラー展開の1次近似なので、精度が悪く、例題以外に用いられることはあまりないのですが考え方が明瞭なので基礎知識として習得されることをお勧めします。

　また、図1を見ると、前進法では現在の変化が続くと考えるのに対して、後退法では変化を先取りしていることが分かります。その結果、曲線の形状に関わらず、

• 前進法は曲線の外側
• 後退法は曲線の内側

を予測することになるのです。

　これらの違いは次のように安定性を考える上で重要な特性なので覚えておいてください。

　解析対象である過渡解析の応答波形は一般的にフーリエ級数に分解し、正弦波の組み合わせで表現できます。ですから正弦波曲線の外側を予測する前進法は時間刻みを粗くすると曲線から乖離（かいり）することになり、条件によっては予測値が「無限大」のような計算不能な結果になることもあります。この現象を「発散する」と言います。あるいはその前駆現象として振動する場合もあります。

　一方、後退法は、図1で示したように、曲線の内側を予測するので振幅が小さくなることはあっても、異常に大きくなることはありません。

　理解を助けるためにいくつか計算をしてみましょう。まず、次の減衰曲線を前進法で解く場合を考えます。

　前進法での計算では時刻t_nの微係数（dY_n／dt＝−Y_n）を使いますので、刻み時間をΔtとすれば

となり、式（2）を見るとY_n＋1の値は現在値Y_nのみから計算していることが分かります。さらには式（2’）の｜1−Δt｜が1以上、すなわち刻み時間Δtが時定数の2倍以上に粗くなると、予測点が累積的に増大し、安定的に計算できないことも分かります（発散）。

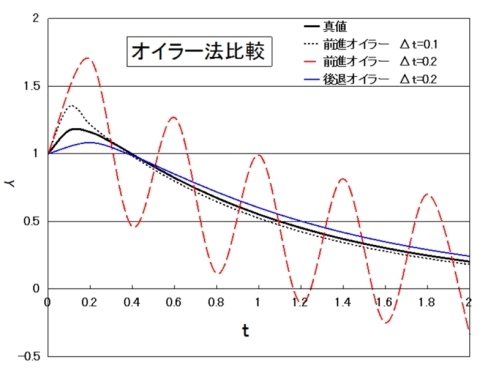
　通常、このような大きな刻み時間を採ることはないのですが、関数が式（3）のような場合には、小さい振幅ではありますが第2項にe^−10tという高周波成分が含まれています。従って、刻み時間Δtを0.2以上にすると図2のように、この高周波成分が振動・発散を起こします。波形の様子だけで関数の成分を見抜くことは難しいと言えます。

図2　解の発散例（クリックで拡大）

　一方､後退法で式（1）を計算した場合は、右辺にもY_n＋1を使った式（4a）や､式（4a）を解いた式（4b）になります｡

　このように､最終的な結果を得る式（4b）を導くには式（4a）を解かねばならないことや、Δtを大きくしても発散することがないことが分かります｡

　式（3）を後退法で計算した例も図2に併記しますが、前進法では振動現象を引き起こす刻み時間（Δt＝0.2）でも、振動を起こさずに安定して曲線の内側を通っています。このように曲線の内側を予測する後退法は振動波形において発散しにくい特徴を持つのです^＊2）。

＊2）ここで説明した特性は高次近似を用いても現れる、いわば本能的な特性なのでよく理解しておく必要があります。例えば、台形法は2次陰解法ですが、良く使われる古典的4次ルンゲ・クッタ法（RK4）は陽解法ですのでご自分のプログラムでRK4を使う場合には刻み時間に注意が必要になることは覚えておいてよいかと思います。

　そして、過渡解析ではどのような応答波形になるかは解析結果を得るまで分かりません。発散しにくく安定性に優れた後退法が回路解析で用いられるのはそのような観点からなのです。

　とはいえ、図2から分かるように刻み幅Δtを大きくすれば後退法でも真値と差を生じ、精度は悪くなります。過渡解析で正しい結果を得るためには、安定性と精度は別物ということを理解し、解析手法によらず時間刻みがいかに重要かを理解しなければなりません。

　なお、結果が十分な精度で得られたか否かを検証するためには、ここまで説明してきたような背景から、時間刻みが十分か否かを確かめなければなりません。そのためには、以下のようなことを行う必要があります。

• 計算ポイント表示機能があれば、振動波形の中の計算ポイント数を確認する
• 計算ポイント表示機能がなければ、別の刻み時間での解析と比較する

　このような結果の検証はSPICEのみならず、有限要素法や有限体積法のツールを使う場合にも要求されます。ですから、われわれ解析技術者は、このような「検証」を常日頃から心掛けなければならないのです。