統計の食わず嫌いを直そう(その8)、統計的に「王様の耳はロバの耳」と言うために:山浦恒央の“くみこみ”な話(80)(4/4 ページ)
2.4.1 μ1 ≠μ2の場合(両側検定)
図.2は有意水準5%の両側検定の場合の、採択域と棄却域をグラフ化したものです。
両側5%の場合は、「検定統計量 < -1.96」、または、「検定統計量 > 1.96」に入るならば(グラフの赤い部分に入るならば)、帰無仮説は棄却されることになり、「王様の耳は国民の耳とは違う(ロバの耳かネズミの耳かはさておき)」であると判断できます。一方、「-1.96<検定統計量 < 1.96」の場合、帰無仮説を採用するため、「王様の耳は国民と同じ」となります。
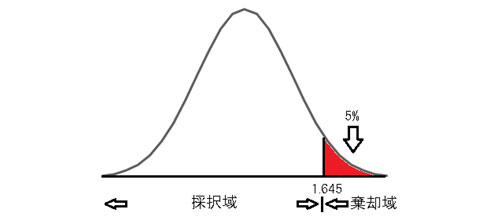
2.4.2 μ1 >μ2の場合(右片側検定)
右片側検定の場合、採択域と棄却域は次のようになります。両側検定と同様に、赤い部分に入っていれば、帰無仮説を棄却でき、白い部分に入っていると帰無仮説が採択されます。すなわち、「王様の耳は国民の耳より長く、ロバの耳である」と判定できるのです。
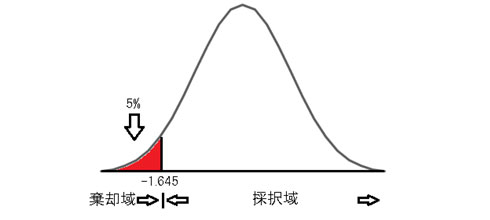
2.4.3 μ1 <μ2の場合(左片側検定)
左片側検定の場合は、次のようになります。よって、統計量<-1.645の場合ならば、帰無仮説を棄却でき、そうでなければ帰無仮説を採択します。
3. まとめ
プロセス改善効果を分析することは重要なことですが、全データから分析を行うことは意外と困難です。今回は、限られたデータを使用した母平均の差の検定の理論的な部分を説明しました。実際に適用する際には、データの数、データの分布、統計式、対応の有無などを考慮する必要があります。
次回は、例題を用いて作業手順を紹介します。
参考文献
『例題で学ぶ初歩からの統計学 第2版』 (白砂堤津耶 著、2015年、日本評論社)
『統計と確率ケーススタディ30―基礎知識と実戦的な分析手法』 (ニュートンムック Newton別冊)
『Excelで学ぶ統計解析入門 Excel2013/2010対応版』 (菅民郎 著、2013年、オーム社)
東海大学 大学院 組込み技術研究科 准教授(工学博士)
関連記事
 統計の食わず嫌いを直そう(その7)、「鎌倉時代の平均ワイン消費量」と「平均値の検定」
統計の食わず嫌いを直そう(その7)、「鎌倉時代の平均ワイン消費量」と「平均値の検定」
「効果がある」と言うためには比較が必要です。新旧開発プロセスの生産性や品質の平均値を比べるためには、「平均値の差の検定」が必要となります。 食わず嫌いを直そう、朝顔の観察日記とデータ収集(その6)
食わず嫌いを直そう、朝顔の観察日記とデータ収集(その6)
難しそうな「統計」ですが、データの分析以上に重要なのが「収集」です。今回は、統計分析の前段階に相当する「データを集める」という部分に焦点を当てて解説します。 食わず嫌いを直そう、「平均値」だけが平均じゃない!(その5)
食わず嫌いを直そう、「平均値」だけが平均じゃない!(その5)
データ解析の王様ともいえる「平均値」ですが、それが本当に母集団の性質を表現しているかは確認すべき事項です。母集団によっては「最頻値」や「中央値」の採用を考慮すべきです。 食わず嫌いを直そう、統計計算の王様「平均値」の落とし穴(その4)
食わず嫌いを直そう、統計計算の王様「平均値」の落とし穴(その4)
思わず身構えてしまう「統計」ですが、手をつけてしまえば何とかなるものです。今回はデータ解析手法の“王様”である「平均」について、解説します。 食わず嫌いを直そう、小学生の知識で統計データを可視化する(その3)
食わず嫌いを直そう、小学生の知識で統計データを可視化する(その3)
「統計」と聞くと頭が痛くなる人も多いかと思いますが、「今持っている知識でも何とかなる」ものです。その第一歩として、簡単なデータの可視化手法について紹介します。
関連リンク
Copyright © ITmedia, Inc. All Rights Reserved.
組み込み開発の記事ランキング
- 低価格FPGAでも文字認識AIの学習は可能なのか
- インフィニオンのSiC-MOSFETは第2世代へ、質も量も圧倒
- パナソニックの電動アシスト自転車にエッジAI機能を提供
- スバルが次世代「EyeSight」に採用、AMDの第2世代「Versal AI Edge」
- 自社開発のRISC-V CPUコアを搭載した32ビット汎用マイコン
- 組み込みシステム向けRTOSのシェアはTRON系が約60%
- CAN通信におけるデータ送信の仕組みとは?
- 東武ストアが指静脈による手ぶら決済を開始、酒類対応でセルフレジ利用率60%も
- CANプロトコルを理解するための基礎知識
- イチから全部作ってみよう(7)正しい要求仕様書の第一歩となるヒアリングの手順
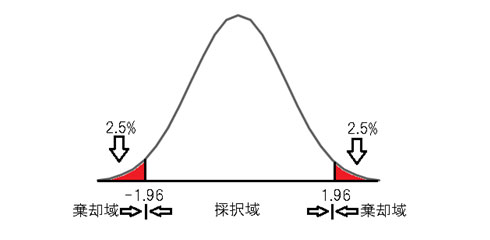 図.2 両側検定の棄却域と採択域
図.2 両側検定の棄却域と採択域