標準偏差って何? 公差設計で生産バラツキを統計学的に考える:3D設計推進者の眼(30)(3/3 ページ)
正規分布と用語――標準偏差とは
さて、一般的によく見られる「左右対称型」の分布の例では、サンプル数を2倍に、データ区分を2分の1にすることで、ヒストグラムの分布は細分化されて、中心的な分布を持ち、そこを頂点とする“滑らかな”山の形に変化しました。サンプル数を増やし、データ区分を狭くする、例えば、測定部品数を「限りなくたくさん、無限大に」、データ区分を「限りなく狭く(細かく)、0に近づけていく」とどうなるのでしょうか。
この場合、その分布は“とても滑らかな曲線を描く形”となりますが、それが「正規分布」です。このような流れの中で、正規分布というものを定義したわけですが、公差計算と公差解析の中で使用する正規分布についてお話する上で、外しては語ることのできない“用語”についてだけ、そのお話をすることにします。
母集団
情報を得たいと考える“モノ”、この例では該当部品の全てを示します。全数検査が義務付けられていれば、全てを測定することになりますが、大量生産を行うような場合は、“抽出”により測定することも多いと聞きます。全てを測定するのであれば、その測定値から得られる平均値や分布は高い精度を得ることが可能です。
サンプル
母集団を構成する全てを測定する場合もあれば、現実的にできない時など母集団の中から“抽出”を行う場合があり、これを「サンプル」としました。このようなサンプルから平均値や分布を得ることで、母集団を想像します。
平均値
平均値はまさに得られた値の平均値ですが、母集団から得たものと、サンプルから得たものは記号によって区別します。また以下のように表します。
- 母集団から得た平均値:μ
- サンプルから得た平均値:x̄
標準偏差
ばらつきの大きさを数値で示したものになります。これもまた、母集団から得たものと、サンプルから得たものを記号によって区別します。
- 母集団から得た標準偏差:σ
- サンプルから得た標準偏差:S
さて、私としては、この「標準偏差」といわれるところから、「ん?」と思うのですが、皆さんはいかがですか?
まず標準偏差の話の前に、「偏差」とは何でしょうか? 偏差とは個々のデータ(例では測定値)とそのデータの平均値の差になります。言い換えると、「個々のデータは平均値からどれだけ離れているか」で、その大きさを表すわけです。
では、個々のデータの全部の偏差を求めた後に、「その平均を取って測定データの偏差の平均を“ばらつきの大きさの平均値”として見てみよう」だなんて考えてみます。実はこれが「標準偏差」になります。
偏差はプラスになる場合も、マイナスになる場合もあります。平均値よりも小さな測定データの偏差はマイナスになり、平均値よりも大きな測定データの偏差はプラスになります。これらの偏差を全て足そうとすると、左右対称型のヒストグラムの分布の形を示している場合、すなわち正規分布となっている場合には、偏差の合計がゼロになってしまうので、全体(母集団であってもサンプルであっても)のばらつきの大きさを示す指標としてはどうにも使えなさそうです。
ということで、偏差を2乗して足し算をすることでゼロにならないようにして、平均を求めたものが、標準偏差となります。ちなみにこの偏差の合計は2乗された値です。単位系も2乗(例ではmm2)になってしまっているので、平方根(√)で元の単位(mm)に戻します。偏差の合計を測定数で割りたいところですが、この標準偏差を求める際の分母は測定の数(母集団の数・サンプルの数)ではなく、測定の数から1個引いた数になります。この数を「自由度」といいます。
自由度
標準偏差を求めるために割る数で、「測定数(母集団数・サンプル数)n−1[個]」というように決まっています。なぜかと理解するのは、私自身難しいのですが、こんなイメージです。
あるサンプルで平均値を求めたとしましょう。例とするとサンプルデータが5個あります。そのサンプルデータの値は見えていませんが、平均値が10という値だということは分かっているとします。では、そのサンプルデータの値を“自由に”決めようとした場合、4個を決めることはできますが、残り1個は4個の値の結果決められるものであって「自由ではありません」ということから「自由度をn−1とした」ということでいかがでしょう。
ということで、標準偏差は次のような数式で表されます。
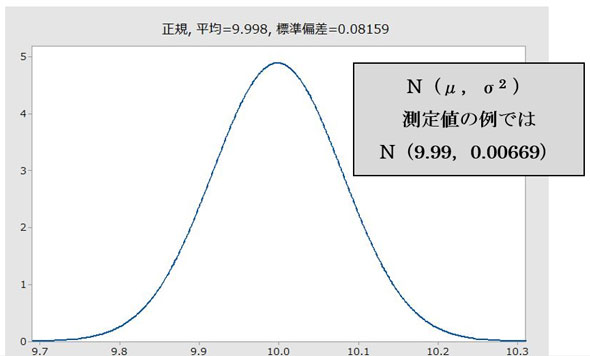
母集団の標準偏差とサンプルの標準偏差は記号で区別するというお話をしましたが、サンプルから得られたものを“正規分布”として“見なす”場合には、これを区別せずに母集団の標準偏差σとして表示します。これがサンプルから母集団を想像するということだと筆者は解釈しています。測定値例でのデータから、平均と標準偏差を求めてみました。
測定値と求めた平均と標準偏差から分布のグラフを作成してみました。なお、グラフ中に別途記載しましたが、正規分布の意味である「Normal Distribution」を示す大文字の「N」とともに平均値μと標準偏差σも合わせて表記してみました。
この表示の中には、標準偏差σの2乗が示されていますが、これは何でしょう? これが「分散」といいます。
分散
簡単にいえば、「標準偏差の二乗=分散」です。「その意味は?」と思うのですが、私の解釈では、偏差は個々のデータが平均からどれだけ離れているかというものに対し、偏差の2乗の和の平均化は、「このサンプルもしくは母集団がどんな状態なのかということを示すのではないかな?」としています。
今回の例ではサンプル数が全ての数を示す母集団になりましたが、サンプルから母集団を想像するという統計学の考え方から正規分布を考えるということもできることができます。正規分布のお話はもう少しだけ続けたいと思います。次回をお楽しみに。
(次回に続く)
関連記事
 「実機レスによりデバッグ完了期間が1週間短縮」は大きいといえるのか
「実機レスによりデバッグ完了期間が1週間短縮」は大きいといえるのか
機械メーカーで3D CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。今回は、フロントローディングとはどういうことなのか、実機レスデバッグの試算例も見ながら考えてみる。 設計者によるPDM導入で大事なフォルダ構成検討
設計者によるPDM導入で大事なフォルダ構成検討
機械メーカーで3次元CAD運用や公差設計/解析を推進する筆者から見た製造業やメカ設計の現場とは。今回は設計者のためのPDMにおける構造について説明する。 開発・デバッグ作業を楽にするFPGA開発環境
開発・デバッグ作業を楽にするFPGA開発環境
前回に引き続き、FPGAの開発環境について解説。FPGAは実機検証ができるだけがメリットではなく、デバッグを楽にしてくれる大きな利点もある KGDBを使って、Android組み込みボードをリモートデバッグしよう!【前編】〜KGDBの仕組みを理解する〜
KGDBを使って、Android組み込みボードをリモートデバッグしよう!【前編】〜KGDBの仕組みを理解する〜
「AndroidのUSB機能」をテーマに、Android搭載の組み込みボードを実際に用いながら、その仕組みなどについて詳しく解説する連載。第2回となる今回は、Linuxカーネルデバッガ「KGDB」の仕組みについて詳しく解説する。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- 有限要素法入門 〜連立方程式の解法、変位の計算〜
- 3σと不良品発生の確率を予測する「標準正規分布表」
- ムダのない作業と楽しさをもたらす“ありそうでなかった発想”
- SUBARUが深層学習によるAI構築ツールを導入、プレス領域の成形解析工数の削減へ
- 幾何公差の基準「データム」を理解しよう
- フローで考える流れのモデリング(その2) 〜適用例と3D/1Dの関係〜
- 計算時間が従来比最大1000倍高速な流体解析ベースのトポロジー最適化ソフト
- 「設計者はなぜCAEを煙たがるのか」を考察し、広がりを阻害する壁を取り除く
- 知らないと取り返しがつかなくなる金型の費用と作製期間の話
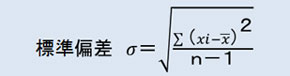
 平均・標準偏差・分散を求めてみた例(構造計画研究所「Minitab17」使用)
平均・標準偏差・分散を求めてみた例(構造計画研究所「Minitab17」使用)