「データム」とは何か？　をあらためて理解する：産機設計者が解説「公差計算・公差解析」（4）（2/3 ページ）

「拘束」という考え方からデータムを意識する

　データムの図面への記入方法については、次回詳しく解説しますが、まず3D CADにおけるモデルの「拘束（自由度を制限する）」という考え方から、データムを意識します。

　座標軸X、Yによって作られる面をXY平面とし、これを「正面」、同様に座標軸X、Zにより作られる面をXZ平面とし、これを「平面」、座標軸Y、Zにより作られる面をYZ平面とし、これを「右側面」とします。まずは、平面に直方体のモデル（図5中の不透明なもの）を置いてみます。

図5　平面上に置かれた直方体形状のモデル

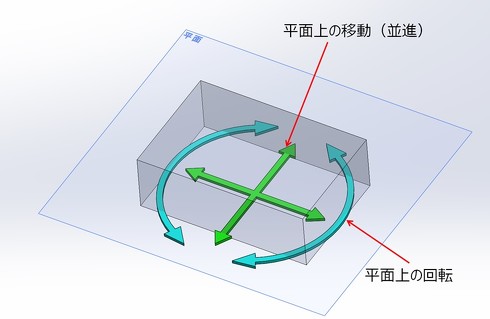
　この平面上に直方体形状のモデルが置かれた状態というのは、

といえます。

図6　平面上に置かれたモデルの並進2成分と回転1成分を図示

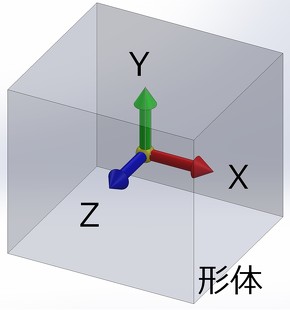
　つまり、モデルが動かないように固定するためには、この自由度を拘束する必要があります。この直方体モデルを平面上に置いただけでは、「自由度は3つある」と説明しましたが、モデルを問わず、空間上にある自由度はいくつあるでしょうか？　なお“空間上”とは、直交3軸の座標系を持つ3次元空間上に形体が浮いていて、形体の重心とその座標系の原点が一致している状態だとお考えください。

図7　空間上の直交座標軸と形体の重心が一致しているモデル

　図7に示した形体は、何にも拘束されていないので、直交する3軸おのおのの座標軸の方向に自由度が3つ、その座標軸の周りの回転自由度が3つ、合計6つの自由度を持っています。

　では、設計、加工、測定の視点で、この形体を「完全に動かないもの ⇒完全に拘束する ⇒形体の姿勢を決める」にはどうしたらよいでしょうか。形体の姿勢を決めるということは、この「6自由度を拘束する」ことになります。

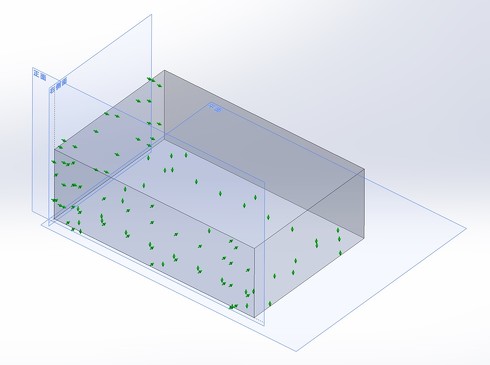
　その上で、形体のデータム平面、実用データム形体を考えた場合、この「幾何学的な直交する3平面」によって形体を拘束できれば、形体の姿勢を決められます。これを「3平面データム系」といい、機械設計で形体の幾何公差を考える上では基本中の基本であると、筆者は理解しています（図8）。

図8　3平面データム系により形体の姿勢を決める（矢印の面により拘束されている）

　また、図9のように軸直線および中心面によって、3平面データム系が構築されるものもあります。

図9　軸直線、中心面による3平面データム系により形体の姿勢を決める

　3平面データム系における各面は「設計意図として最初の基準は何か、その次は、またその次は……」というように、3平面の中でも優先順位があるはずです。つまり、設計者は設計段階で、原材料をどのような手順で加工すべきかを意識する必要があり、さらには部品を組み立てる際の基準とその組み立て方に関しても考慮しなければなりません。

　測定の場合も同様です。このように決められた基準を使用することで、図面に記載されたサイズ公差、幾何公差を正しく測定できます。