さまざまな幾何公差【その2】〜その定義や例、測定方法について〜:産機設計者が解説「公差計算・公差解析」(7)(1/3 ページ)
機械メーカーで機械設計者として長年従事し、現在は3D CAD運用や公差設計/解析を推進する筆者が公差計算や公差解析、幾何公差について解説する連載。第7回は前回に引き続き、“具体的な幾何公差”について取り上げる。
前回に引き続き、今回もさまざまな「幾何公差」について解説を進めます。
1-4.円筒度(Cylindricity)
「円筒度」とは何でしょうか。JIS規格(日本工業規格)によると「円筒形体の幾何学的に正しい円筒からの狂いの大きさ」と定義されています。前回、「真直度」と「真円度」について取り上げましたが、これらについて筆者は「真円の規制と真直(同軸)の規制の両方」、もう少し分かりやすくいうと「まん丸で真っすぐな状態」と解釈しています。
「円筒」というと、陸上競技のリレーで使う「バトン」のような形を想像しますが、要するに「底面と上面が正円の立体図形のこと」を示します。「円柱」といった方がイメージしやすいかもしれません。
円筒度は、真直度と真円度という2つの定義を持つため、その測定も難しそうですが、設計意図を示すものとして設計者視点で捉えても難解です(筆者のイメージですが)。
ちなみに、円筒度の使用例ですが、高い回転精度が求められる工作機械の主軸に用いられるベアリング(軸受け)、さらには軸やハウジングに対して円筒度が要求されると筆者は解釈しています。ただし、筆者自身、こうしたケースでは真円度、同軸度、円周振れを用いているため、円筒度の使用実績はありません。
公差域の定義
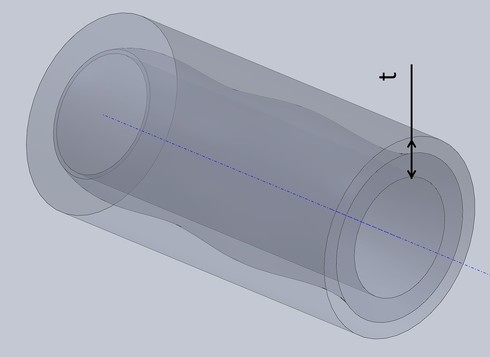
公差域は「tだけ離れた同軸の2つの円筒」によって規制されます(図1)。
例
図2をご覧ください。この場合、円筒表面は半径距離「0.1」だけ離れた同軸の2つの円筒の間になければならないことを表しています。
円筒の表面に円筒度を示す場合、表面形体への指示になります。このため、直径の寸法線と指示線の矢を外し、幾何公差値にΦは付けません。
測定方法
測定方法については、3次元測定機や真円度測定機などを使用します。
輪郭度
続いて「輪郭度」です。「輪郭」とは、国語としての意味では「物の周囲を形作っている線」になります。「アウトライン」ともいえますが、JIS規格では「線の輪郭度」と「面の輪郭度」の定義があります。筆者は利用したことがありませんが、デザイン性のあるものに対する用途が多いのではないでしょうか。
1-5.線の輪郭度(Profile of a Line)
公差域の定義
まずは、線の輪郭度についてです。JIS規格では「理論的に正確な寸法によって定められた、幾何学的に正しい輪郭(以下、幾何学的輪郭という)からの線の輪郭の狂いの大きさをいう」と定義されています。線の輪郭度の評価対象となる形体は、1本の自由曲線、1本の直線ということになります。
例
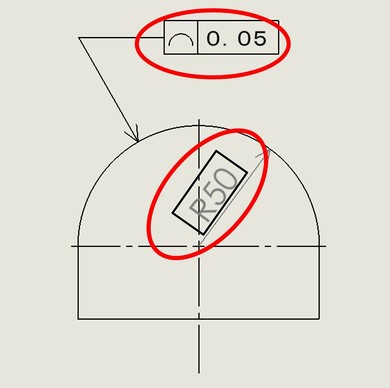
自由曲面に線の輪郭度を指示する場合、母線への指示になります。その形体の理論寸法を表す寸法線とともに使用します。□(四角)で囲んだ寸法は、理論的に正確なサイズを示します。
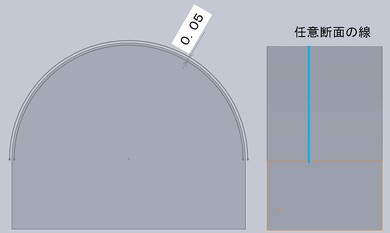
この例では、指定の曲面を切断した任意の断面の線が公差域「0.05」以内に入っていればよいことを表しています。任意断面ですので、この線の輪郭度は任意の2次元領域を示すことになります。
測定方法
3次元測定器を使用するやり方の他、投影機による測定方法もあります。筆者は投影機を使用して特殊な歯形を計測した経験がありますが、トレースは手作業になりますので手間が掛かります。
また、ピントの合わせ方によって測定結果が変化したり、照明の当て方、光量によってエッジの見え方が変わったりすることもあります。そのため、これらは測定誤差を引き起こす原因にもなっています。
Copyright © ITmedia, Inc. All Rights Reserved.