動くものを解析してみる：初心者のための流体解析入門（9）（2/3 ページ）

有限体積法で何を解いているのか？

　基本的な考え方は以上ですが、ここで、流体解析で“何を解いているのか”を振り返ってみましょう。流体解析に使用される離散化の手法は1つではありませんが、一般的なものとして「有限体積法」が挙げられます。

　では、有限体積法では何を解いているのでしょうか？　構造解析で一般的な手法は「有限要素法」ですが、構造解析で有限要素法を使用する場合、要素ごとに剛性マトリクスの求解を行います。その結果として変位がまず求まり、それからひずみ、応力を求めていきます。

　有限体積法の場合は、要素ごとに運動量保存則を解いていきます。要素に蓄積される運動量とは、「流れに乗って要素に入ってくる運動量」と「流れに乗らずに要素に入ってくる運動量」の和で表現できます。

図2　運動量保存則　［クリックで拡大］

　「流れに乗らずに要素に入ってくる運動量」とは、別の言い方をすると「応力」です。構造解析で耳なじみのある言葉ですね。この運動量には、圧力によるものと粘性によるものがあり、構造解析的に耳なじみのある言葉としては、直応力とせん断応力になります。これらの応力は、あくまでも周囲の要素との相対的な関係によってのみ決まるものなので、要素の移動は関係ありません。

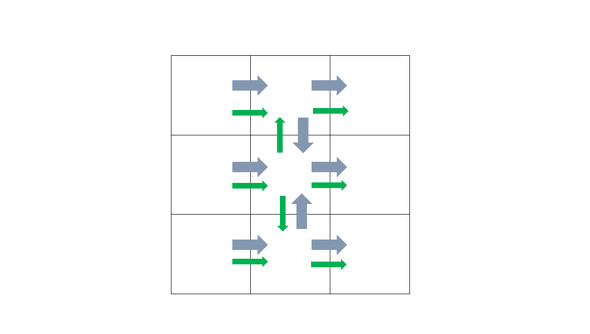
　それに対して「流れに乗って要素に入ってくる運動量」は、「移流成分」と呼ばれるものになります。こちらの運動量は、要素と流体の相対速度から構成されるので、要素移動の影響を受けることになります。自分が要素の中にいるとしましょう。例えば、要素が静止している解析で、流れが左から右に流れていくのであれば、運動量も左から入り、右から出ていくことになります。

　では、要素が流れと同じように左から右に動いているとしましょう。この場合、運動量は要素移動の速度に依存します。流れの速度よりも速く右方向に移動しているとしたら、むしろ運動量は右から入って左から出ていくように見えることになります。つまり、この運動量は“要素移動の状況に依存する”ということになります。ということなので、このような要素移動を伴う解析においては、移流による影響を流れと要素の相対速度に置き換えて考えるのです。