位置度を考える上で重要な「最大実体公差」：産機設計者が解説「公差計算・公差解析」（13）（3/4 ページ）

2つの部品のアセンブリを例に最大実体公差を考える

　これら2つの部品（部品Aと部品B）は図5のように「軸と穴のはめ合い」に多く適用されます。

図5　最大実体公差（アセンブリ例） ［クリックで拡大］

　それでは、この図5のように、2つの軸が加工される部品と、2つの穴が加工される部品の組み合わせ（アセンブリ）を行う場合を例に、最大実体公差方式について考えてみましょう。

　設計者は、組み立て部門の要求を受けて次のように考えます。

図6　軸部品と穴部品は最大実体サイズ。位置度公差内で、軸の中心距離が公差範囲内で広く、穴の中心距離が狭い場合 ［クリックで拡大］

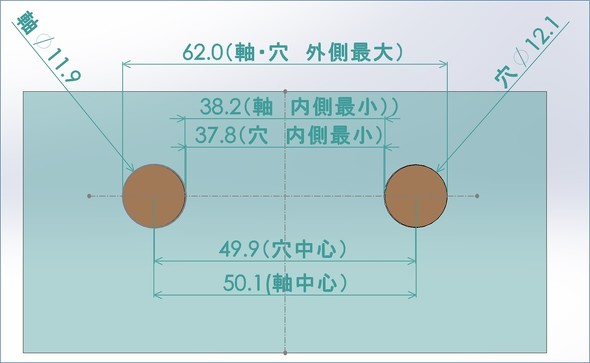
　図6は、軸と穴が最大実体サイズの場合で、軸の中心距離が最大、穴の中心距離が最小となる場合を示しています。このとき、軸の外側最大サイズは

（軸の中心距離最大値）50.1［mm］＋（軸の最大実体サイズ）11.9［mm］＝（軸の外側最大サイズ）62.0［mm］

となります。また、穴の外側最大サイズは

（穴の中心距離最大値）49.9［mm］＋（穴の最大実体サイズ）12.1［mm］＝（穴の外側最大サイズ）62.0［mm］

となります。これは、軸と穴の関係を見たとき、その外側最大の位置では「ガタ」はないものの、軸は穴に“はめる”ことができる状態であることを示しています。

図7　軸部品と穴部品は最小大実体サイズ。位置度公差内SW、軸の中心距離が公差範囲内で広く、穴の中心距離が狭い場合 ［クリックで拡大］

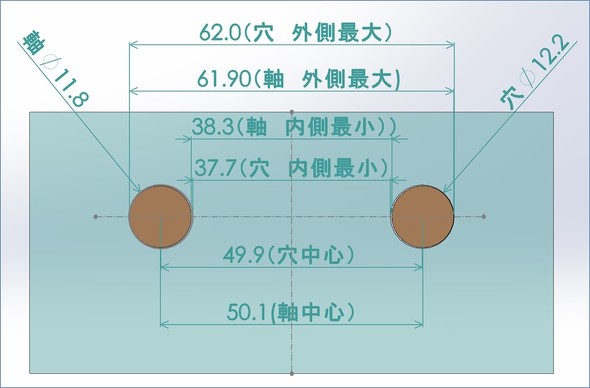
　図7は、軸と穴が最小実体サイズの場合で、軸の中心距離が最大、穴の中心距離が最小となる場合を示しています。先ほどと同様に、軸と穴の関係を見ると

（軸の中心距離最大値）50.1［mm］＋（軸の最小実体サイズ）11.8［mm］＝（軸の外側最大サイズ）61.9［mm］

となります。また、穴の外側最大サイズは

（穴の中心距離最大値）49.9［mm］＋（穴の最小実体サイズ）12.2［mm］＝（穴の外側最大サイズ）62.1［mm］

となります。これは、軸と穴の関係を見たとき、その外側最大の位置では、62.1［mm］−61.9［mm］＝0.2［mm］の「ガタ」が生じていることを示し、軸は穴に“はめる”ことができる状態です。

　最小実体サイズに注目したとき、この「ガタ」を詰めても「はめ合い」の機能には問題は生じません。つまり、このガタには「マージン」があるともいえます。そこで、軸と穴を規定する位置度公差に注目し、このマージンを公差域に対して加味して考える設計方法のことを、「最大実体公差方式」といいます。