構造解析、いろいろあれど……:構造解析、はじめの一歩(3)(1/3 ページ)
「構造解析」を“設計をより良いものとするための道具”として捉え、実践活用に向けた第一歩を踏み出そう。第3回は、構造解析の種類について詳しく解説する。
フックの変形を考えてみる
一言で「構造解析」といってもその範囲は非常に広いです。
1つの部品を例として考えてみましょう。ここでは、カバンやコートを掛けるフックを想定します。その部品に何らかの力が掛かったとします(図1)。
フックは壁に「完全」に固定されているとします。
ここで「完全」を強調したのには理由があります。現実の世界では、「完全」に固定されることは、まずあり得ません 。フックを取り付ける壁の素材や、フックの取り付け方が、フックの挙動に大きく影響します。フックにカバンやコートを掛けると、フックの上側には隙間が開きますし、フックの下側は壁にめり込みます。
部品は何らかの方法で必ず固定されます。空中に浮いている部品はありません。部品を固定することを構造解析では「拘束条件」と言います。この拘束条件が構造解析の結果に大きく影響を与えます。その詳細については、本連載の中で解説します。
さて、フックに話しを戻しましょう。フックに掛けるカバンやコートのことを「荷重」と言います(「加重」ではありませんので、お間違えのないように)。荷重の掛かっていないフックは変形していません。地球には重力があるので、ホントはほんの少しだけ変形しています。これを「自重」と言います。「自らの重さ」というわけです。
フックの丈夫さに対して重さは十分に軽いので、自重によるフックの変形は全くと言っていいほどありません。重量があるものや、大きな加速度を受ける部品や構造物は、自重の影響を無視できない場合がありますので、自重は常に意識しておいてください。
というわけで、今回のフックの例では、「自重(=地球の重力)」の影響は考えないこととします。
フックの変形と荷重の関係
荷重の大きさによって、フックの変形量は変わります。それだけでなく、荷重を取り去った後のフックの状態も変わってきます。
フックに荷重が掛かっていない場合
フックに荷重が掛かっていない場合は、もちろん何の変形もしていません。
フックに荷重を掛けて、その後荷重を取り去る場合
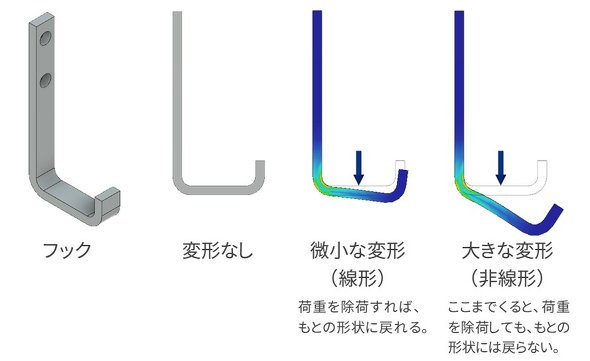
■荷重が十分小さい場合
フックに十分小さな荷重を掛けるとフックは変形します。フックの素材が鉄のような金属だとフックの変形は目で見ることはできません。フックの素材が樹脂のようなものであれば、わずかながら変形が目に見えるかもしれません。
フックに掛けた十分小さな荷重を取り去ります。フックは元の形状に戻ります。
■荷重が大きい場合
フックに大きな荷重を掛けるとフックは変形します。これは荷重が小さいときと同じですが、変形の度合いが異なります。荷重が大きい場合は変形も大きくなります。掛けた荷重とフックの変形の度合いは比例します。
フックにとって、ここが大きな分かれ道となります。
大きな荷重を掛けると、フックが壊れる場合があります。金属製のフックであれば、大きく変形し、荷重を取り去ってもフックは元の状態には戻りません。少しだけ元の状態に戻ろうとはしますが、完全に元の状態には戻りません。ユーザーから見れば「フックが曲がった……」ということになります。樹脂製のフックであれば、折れてしまうでしょう。
これに対し、フックに掛けた大きな荷重を取り去ると、完全に元の状態に戻る場合もあります。ユーザーから見れば「丈夫なフックだっ!」ということになります。
荷重を掛けて、荷重を取り去ったとき(「除荷」と言います)、変形が完全に元に戻る範囲の挙動を「線形」と言います。荷重と変形の比例を超えるその先のことを「非線形」と言います。
線形と非線形については、以前の連載記事「材料が白旗を揚げる『降伏点』とは」の中に、針金ハンガーの動画がありますので、そちらをご覧ください。一目瞭然です。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 知らないと取り返しがつかなくなる金型の費用と作製期間の話
- 3σと不良品発生の確率を予測する「標準正規分布表」
- 幾何公差の基準「データム」を理解しよう
- Excelを使って周波数分析をやってみよう!
- AI活用機能を強化した「AutoCAD 2025」「AutoCAD Plus 2025」をリリース
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- 「データム記号」の使い方と設計者が身に付けておくべき作法
- 位置度を考える上で重要な「最大実体公差」
- FreeCADってどんな3D CAD? 簡単なモデリングから始めてみよう
- 3D機構検証ソフトの最新版、干渉検証漏れ防止機能を搭載