設計者CAEによる締結部の設計法:設計者向けCAEを使ったボルト締結部の設計(7)(1/4 ページ)
部品の固定(締結)のために使用する“ボルトの設計”をテーマに、設計者向けCAE環境を用いて、必要とされる適切なボルトの呼び径と本数を決める方法を解説する。連載第7回では、本連載の最終目標である設計者が使うCAE環境で、必要とされるボルトの呼び径と本数を決める設計法を取り上げる。
本連載の最終目標である、設計者が使うCAE環境(「設計者CAE」の範ちゅう)で、必要とされるボルトの呼び径と本数を決める方法を解説します。設計者CAEでは、複数部品によるアセンブリではなく単品解析を前提とします。単品解析なので接触要素は使いません。また、連載第2回で「もうボルトの谷底は降伏している」といいましたが、ここでは弾性解析で行います。
本設計法の適用範囲
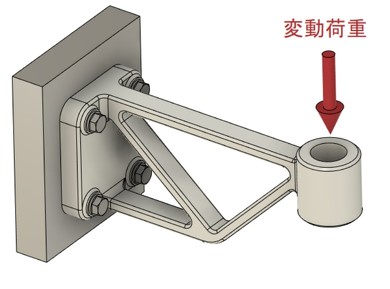
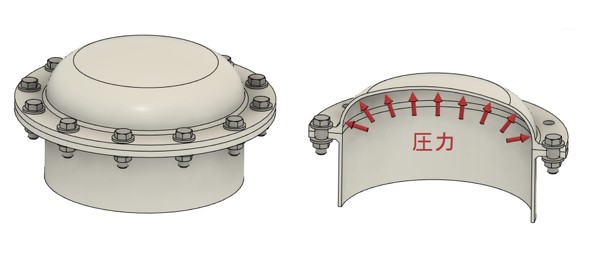
ここで述べる設計法は、図1に示すようなブラケットの先端に変動荷重が作用する場合や、図2に示すようなタンク内の液体が圧力変動する場合などを想定しています。タンクの中の流体が気体の場合や、大気圧にしたら沸点を超えるような温度の液体(容器が破裂するとき、この液体は蒸気である気体になります)の場合は、圧力容器となりますので、そちらの設計指針に従ってください。
軸力を求めるときの摩擦係数
連載第3回で「ボルトが疲労破壊しない条件は、変動荷重が作用したときに被締結体同士が離れないこと」と述べました。締め付けた後のボルト軸力が大きければ被締結体同士が離れにくくなるので、大きな軸力が必要ですが、連載第6回で述べたトルクが上限となります。このときの軸力の求め方も連載第6回で説明しました。
連載第5回で摩擦係数が0.10〜0.26[-]の範囲でばらつくことを説明しました。締め付けトルクを決めるときは、厳しめに考えて大きな応力、つまり大きな軸力が発生するような条件にしなければなりません。よって、摩擦係数は小さい値を採用し、0.10[-]としました。
一方、組み立て後の被締結体同士が離れるかどうかの判断では、悲観的に考えて摩擦係数がばらついて軸力が小さくなってしまったと考えます。摩擦係数が大きいと同じ締め付けトルクでも小さな軸力になりますので、軸力を求めるときの摩擦係数は大きめの値を採用します。ここでは、摩擦係数として0.26[-]を採用します。摩擦係数をご自身で把握されている場合は、変動範囲内で大きい方の値を採用してください。
単純な荷重が作用する場合
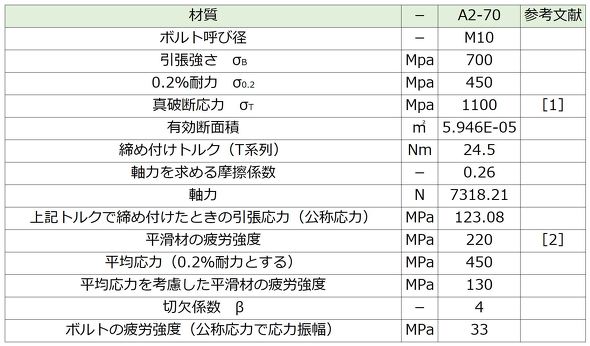
被締結体が離れるか、離れないかの予測には、接触要素を用いたシミュレーションが必要です。設計者CAEの範ちゅうで、これと同等の結果を得るための方法を立案しましょう。M10のA2-70ステンレスボルトを例に説明します。諸元を表1に示します。上記の摩擦係数とT系列によるトルクを採用すると、軸力は7318.21[N]、ボルトの疲労強度は33[MPa]となりました。
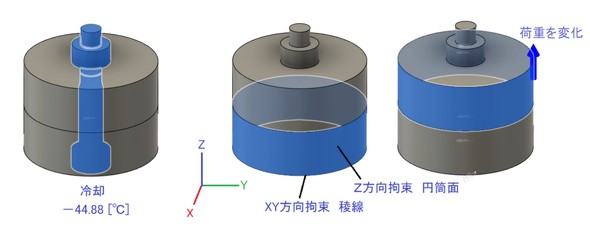
連載第3回を思い出します。図3に、ボルトによる軸力が発生している状態で被締結体に荷重を与えた状態を示します。表1から上記トルクで締め付けたときの引張応力(応力集中を考慮しない公称応力)は123.08[MPa]なので、ボルトにこの応力を発生させるために、ボルトを20[℃]から−44.88[℃]に冷却し、かつ上側被締結体にいろいろ変化させた引張荷重をかけて解析します。
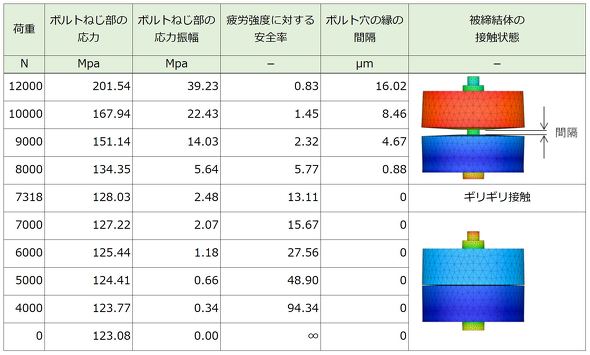
解析結果を表2に示します。ボルト穴の縁の間隔に注目します。これがゼロでなくプラスの値となったら被締結体は離れています。荷重が7318[N]で被締結体同士が離れます。ボルトが1本だけで、荷重が単純な引張荷重なので、ボルト軸力と等しい荷重が作用したときに被締結体同士が離れます。当たり前ですね。荷重7000[N]のときのボルト穴の縁の間隔をゼロと表記しましたが、実は−0.088[μm]と出力されていました。接触圧力が発生しているとき、接触要素では「食い込み」という現象が発生していて、間隔がマイナス値として出力されます。マイナス値のときは接触していることを意味しています。
ボルトねじ部の応力振幅は式1で計算しました。
疲労強度に対する安全率は式2で計算しました。
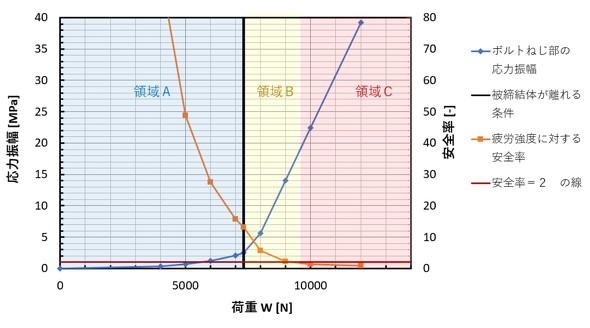
連載第3回でも説明しましたが、応力振幅と安全率をグラフにしました。これを図4に示します。図4中央の黒色の線は、被締結体がちょうど離れる部分です。この点での安全率は13.11[-]です。「被締結体が離れないことが疲労破壊しない条件だ」と述べましたので、被締結体が離れないところ、つまり黒色の線の左側(領域A)で締結部を設計します。
以上の検討では、接触要素を使っていました。では、設計者CAE環境(単品解析)でボルトが疲労破壊するかどうかを調べるためには、どのような解析モデルを作ればよいでしょうか。このようなモデルを「設計者CAEモデル」と呼びます。
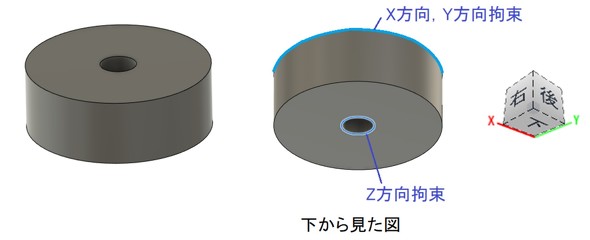
解析モデルは図5に示すように、被締結体の上側だけを解析対象とします。単品解析になりますね。拘束条件を図6に示します。拘束条件は、(1)被締結体同士が接触する側のボルト穴の稜線(りょうせん)におけるボルト軸の方向(今回はZ方向)の変位を拘束します。また、それだけでは解析対象が剛体変位をするので、(2)どこか適当な稜線(この場合は図示した稜線)のX方向とY方向の変位を拘束します。
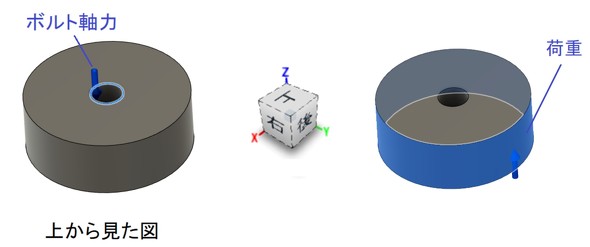
次は荷重条件です。まず(1)ボルト軸力(7318[N])をボルトの頭が接触する側のボルト穴の稜線に、ボルト軸方向(今回は−Z方向)にかけます。これを図7に示します。続いて、被締結体に作用する荷重をかけます。今回は(2)被締結体の円筒面に+Z方向にかけました。荷重値は説明のため0〜1万2000[N]まで変化させて解析しました。
被締結体が離れるかどうかの判定は、図6のZ方向変位を拘束したボルト穴の稜線の反力を有限要素法ソフトから読み取ります。荷重を4000[N]として読み取った例を図9の左側に示します。
反力は88.86[N]とプラス値で、“反力がプラス値ならば被締結体が離れないと判断できます”。ここがポイントです。
拘束点の反力が読み取れないCAEソフトの場合、ボルト穴稜線近傍のZ方向応力成分を表示させてマイナス値、つまり圧縮応力ならば同様の判定結果となります。図9右側はZ方向応力分布です。今回の場合は−150.2[MPa]で圧縮応力でした。
接触要素を用いたモデルでボルト穴稜線の間隔(表3の間隔)と、設計者CAEモデルで求めた拘束部反力(ボルト穴稜線のZ方向反力)の最小値を、図10のようにグラフにしました。図10中央の黒色の線は、被締結体が離れる条件、つまりボルト軸力と外力が等しい線です。青色の線はボルト穴稜線の間隔で、荷重を上昇させると黒色の線を境に急上昇します。つまり、被接触体が離れます。オレンジ色の線は拘束部反力の最小値で、黒色の線を境にプラスからマイナスに転じています。
設計者CAEモデルで、ボルトが疲労破壊しない条件を以下に示します。
被締結体のボルト穴稜線を固定し、ボルト穴稜線のボルト軸方向反力がプラス値ならば被締結体が離れないことに相当し、疲労破壊しないと判断できる。
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 3σと不良品発生の確率を予測する「標準正規分布表」
- 若手エンジニアにありがちな強度設計ミス【前編】
- 知らないと取り返しがつかなくなる金型の費用と作製期間の話
- 幾何公差の基準「データム」を理解しよう
- Excelを使って周波数分析をやってみよう!
- AI活用機能を強化した「AutoCAD 2025」「AutoCAD Plus 2025」をリリース
- 「データム記号」の使い方と設計者が身に付けておくべき作法
- FreeCADってどんな3D CAD? 簡単なモデリングから始めてみよう
- 位置度を考える上で重要な「最大実体公差」
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用

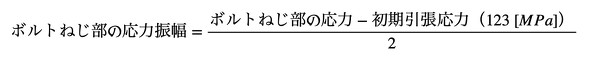 式1
式1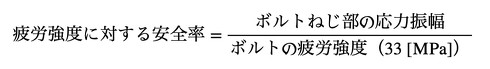 式2
式2