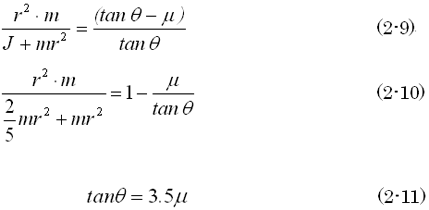摩擦係数というより摩擦係数の変数だ:ピタゴラスイッチの計算書を作ろう(2)(1/4 ページ)
摩擦係数μは、斜面を滑りながら転がっているか、または滑らずに転がっているかにより意味が異なるって理解していた?
銀二さん、再来
前回の話から1週間後、某県の某企業での技術相談を終えた銀二叔父さんは、また草太の下宿先にやって来ました。ピタゴラスイッチのスロープの設計をどうやって行うのか、前回の続きを説明しにやってきたのです。
銀二「この間は途中で帰って済まなかったね。久しぶりにカミサンと神戸で食事をしてきたよ」
草太「50歳を超えてまだ奥さんとデートですか。仲のいいことで、よろしおまんな」
銀二「焼くな、焼くな。ところで、ピタゴラスイッチのスロープの設計の話の続きだったね」
X年度 卒業設計課題(亜津戸大学 工学部 物田研究室)
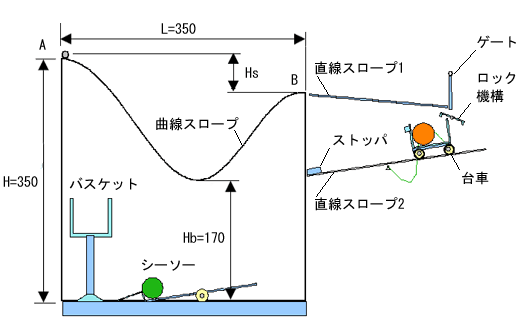
図のようなピタゴラスイッチを設計・製作し、設計計算書と試作品を提出せよ。
A地点から出発したボールは曲線スロープを経てB地点に到達し、直線スロープ1の終端のゲートを通過した後、直線スロープ2に繋留(けいりゅう)している台車のロックを解除する。
繋留が解除された台車は直線スロープ2を降り、ストッパによって横転し、台車の中のボールがシーソーに落下して、反対側のバスケットボールを跳ね上げ、バスケットの中に入るものとする。
なお、曲線スロープの出発地点Aの高さHとスロープの底の高さHb、曲線スロープの長さLは図示した値とし、また、B地点を通過するときのボールは極力遅くなるように設計すること。
ボールはスロープの出発地点Aから終点Bに移動する間にエネルギーを失います。それを補うために位置エネルギーHsが必要ですが、その値をいくらにしたらいいか、というのが、サブ・システム1の曲線スロープの設計のメインテーマでした。つまり、「スロープを通過するときのボールの損失エネルギー」を求める必要がありました。
移動する物体の形状が矩形ならば斜面の上を滑るだけですが、課題ではボールです。つまり、回転運動も考えなければいけない、ということでしたね。
編集部より、読者の皆さまへ
以降で出てくる数式をメモ帳やノートなどに書き取るなどして、実際に計算しながら読み進めてみてください。より理解が深まります。
銀二「ボールは球だから転がる。当たり前だね。ただし、転がると同時に滑る場合もある。だから球の場合には、回転運動と並進運動についての運動方程式を同時に考えなければならないんだ」
草太「運動方程式ね」
銀二「図2.1から回転についての運動方程式は、ボールの半径をr、角速度ω、慣性モーメントJ、傾斜角度θ、ボールと斜面との摩擦力をFとして、以下のようになるのはいいよな」
草太「『オイラーの運動方程式』とかナントカいったよね。摩擦力によってモーメント r・F が働くんだね。それによってボールが回転する」
銀二「よく知ってるね。まったく勉強してこなかったわけではないんだな。ところで前回説明したボールの並進運動といまの(2-1)式からボールが滑らずにスロープを降る条件を求めることができるんだけど、分かるかい?」
草太「質量mのボールの重心についての並進運動の運動方程式は、傾斜角θの斜面に沿って動く速度vに対して、こうだったね」
草太「(2-1)と(2-2)とから摩擦力F を消去すると、こうなるでしょ」
草太「ところでボールはスロープを滑らないんだから、ボールとスロープとの接触点の速度は0だね。ボールは回転しているから、ボールの中心を基準にするとマイナスの方向にrωの速度を持っている。それに対してボールの中心速度がプラス方向にv。だから接触点の速度vpの式は、
vp = v - rω
となるね。だからこの式が成り立つんだ」
草太「つまり前回の(1-3)の関係が成り立つんだね。(2-3)にこの関係を代入すると、こう」
草太「で、さて叔父さん、これからどうするん?」
銀二「(2-2)式の摩擦力Fは未知数かい?」
草太「そういえばFは摩擦力だから、摩擦係数をμ、斜面からボールが受ける力をNとして、
F =μN
だよ。
そして、N はmg・cosθだね」
銀二「じゃあ、いまの式を(2-2)に入れてごらん」
草太「なになに……」
草太「ここで、(2-4)を使って並進速度vを回転の角速度ωで表現すれば(2-6)は、(2-7)式のようにになるでしょ」
草太「(2-5)も(2-7)もωについての運動方程式だけど、未知数ωに対して2つの式が出てきた。これっておかしくない?」
銀二「別におかしくないよ。2つの式が同時に成立するっていうことは、2つの式は実は相似のはずなんだよ。だから、以下の式が成立するはずだ」
草太「ボールが斜面を滑らずに転がるためには、回転運動と並進運動の各方程式が相似である必要があるってことか。イメージとしては回転運動と並進運動が同期しているって感じかな」
銀二「おお、そのとおりだ。なかなかうまい例えじゃないか」
ボールが斜面を滑らず転がるための条件
銀二「ところで球体の慣性モーメントは前回の(1-4)で紹介したように、以下のように与えられるから……」
銀二「(2-8)に(1-4)を代入して計算すると、こう」
草太「ボールがスロープを転がるときには必ず(2-11)が成立していなければならないということ? (2-11)を満足しない場合はどうなるの?」
銀二「傾斜角度θと摩擦係数μが(2-11)を満足しない場合は、ボールはスロープを滑りながら回転するということになるんだ」
草太「設計課題のピタゴラスイッチのスロープの傾斜角θは一定じゃないけど、摩擦係数μの値は一定でしょ? すると特定の傾斜θの場所でしか(2-11)を満足しないことになるよ。つまり、ボールは一瞬だけ滑らずに転がるけど、大部分の場所では滑っていることになる。すると、『転がりながらボールが移動することなんてほとんどない』ってことになるよ」
Copyright © ITmedia, Inc. All Rights Reserved.
メカ設計の記事ランキング
- 3σと不良品発生の確率を予測する「標準正規分布表」
- 知らないと取り返しがつかなくなる金型の費用と作製期間の話
- 若手エンジニアにありがちな強度設計ミス【前編】
- 幾何公差の基準「データム」を理解しよう
- Excelを使って周波数分析をやってみよう!
- AI活用機能を強化した「AutoCAD 2025」「AutoCAD Plus 2025」をリリース
- Formlabsが新型3Dプリンタ「Form 4」発表、LFSを超えるプリントエンジンを採用
- 「データム記号」の使い方と設計者が身に付けておくべき作法
- 位置度を考える上で重要な「最大実体公差」
- FreeCADってどんな3D CAD? 簡単なモデリングから始めてみよう
 ピタゴラスイッチ
ピタゴラスイッチ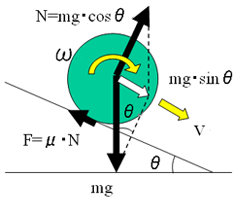 図2.1 ボールの斜面の運動
図2.1 ボールの斜面の運動